题目内容
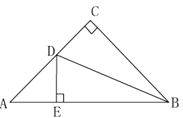
【题目】如图,已知:在△ABC中,∠C=90°,AC=BC,BD平分∠CBA,DE⊥AB于点E.
求证:AD+DE=BE.
【答案】证明见解析.
【解析】试题分析:(1)由∠DEB=∠C,∠EBD=∠CBD,DB=DB可得△DEB≌△DCB,所以BC=BE,又因为AC=BC,所以AC=BE,由题意可得,△ABC为等腰直角三角形,故不难得出△ADE为等腰直角三角形,所以AE=DE,所以AD+DE=AD+DC=AC=BC=BE.
试题解析:
∵BD平分∠CBA,
∴∠EBD=∠CBD,
∵DE⊥AB,
∴∠DEB=90°,
∵∠C=90°,
∴∠DEB=∠C,
在△DEB和△DCB中:
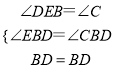 ,
,
∴△DEB≌△DCB(AAS),
∴DE=DC,BE=BC,
∵AD+DE=AD+DC=AC=BC,
∴AD+DE=BE.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目