Question

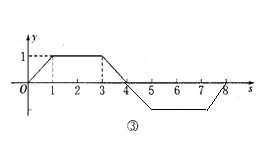
【题目】在平面直角坐标系中，一动点P(x，y)从点M(1，0)出发，沿由A(－1，1)、B(－1，－1)、C(1，－1)、D(1，1)四点组成的正方形边线(如图①所示)按一定方向运动．图②是点P运动的路程s(个单位)与运动时间￡(秒)之间的函数图象，图③是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分．

（1）s与t之间的函数关系式是_______．

（2）与图③相对应的点P的运动路径是_______；点P出发______秒首次到达点B处．

（3）写出当3≤s≤8时，y与s之间的函数关系式，并在图③中补全函数图象．

Answer 1

【答案】（1） (t≥0) ；

（2）M→D→A→N，10；

（3）当3≤s<5时，y=4－s；当5≤s<7时，y=－1；当7≤s≤8时，y=s－8.补全图象见解析.

【解析】试题分析：（1）待定系数法求正比例函数.(2)由图象信息可知.

试题解析：

(1)图象过设s=kt（k）过（2,1）点，所以 (t≥0) .

(2) M→D→A→N 10

(3)设函数是y=ks+b(k.

当3≤s<5时，设图象过（3,1）（4,0），

,解得,

y=4－s；

当5≤s<7时，y=－1；

当7≤s≤8时，过（7，-1），（8,0），

,

解得,

y=s－8.