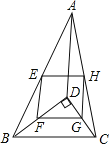��Ŀ����
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P��ͼ��N���������¶��壺���QΪͼ��N��һ�����㣬P��Q������������ֵΪdmax��P��Q�����������СֵΪdmin�����ǰ�dmax + dmin��ֵ�е�P��ͼ��N��ġ��;��롱������d��P��ͼ��N����
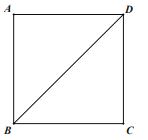
��1����ͼ��������ABCD������Ϊ��O��A(3��3)��
�� ��O���߶�AB�ġ��;��롱d��O���߶�AB��= ��
�� �����������y�ύ�ڵ�E��F����P���߶�EF�ϣ�d��P��������ABCD��=7�����P�����꣮
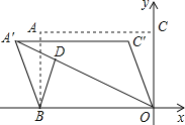
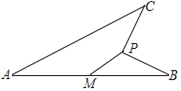
��2����ͼ2���ڣ�1���������£���C��D����������CD������AC����M������CD�ϵ�һ�㣬���![]() d��M���߶�AD��
d��M���߶�AD��![]() ��ֱ��д��M�������tȡֵ��Χ��
��ֱ��д��M�������tȡֵ��Χ��
���𰸡���1���� ![]() ����(0��1)��(0��-1)����2��
����(0��1)��(0��-1)����2��![]()
��������
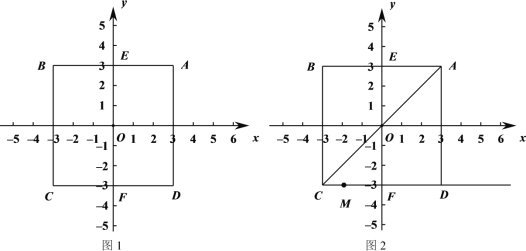
(1)�ٸ��ݡ��;��롰�Ķ�����㣺OE�������������Сֵ��OA�����������ֵ����ӿɵý��ۣ�
�ڷ����������P��y���������������ϣ����ݡ��;��롰�Ķ��壬����d(P��������ABCD)=7���з��̼��㼴�ɵã�
(2)��M���߶�CD�Ϻ��ӳ�����������������á��;��롱�Ķ����з��̿ɵý��ۣ�
(1)����ͼ1������OA��
���ı���ABCD�������Σ���A(3��3)��
��dmax+dmin=OE+OA![]() ��
��
��d(O���߶�AB)=![]() ��
��
�ʴ�Ϊ��![]() ��
��
����P(0��![]() )��
)��
��d(P��������ABCD)=7��
��dmax+dmin=7��
�����������
��E(0��3)��F(0��-3)����P���߶�EF��һ�����㣬
��P��![]() ���Ϸ�ʱ����ͼ2������PC��
���Ϸ�ʱ����ͼ2������PC��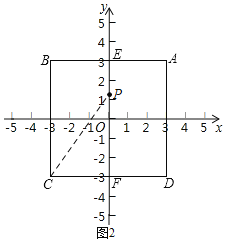
��dmax+dmin=PE+PC=7��
��![]() ��
��
��ã�![]() ��
��
��P(0��1)��
��P��![]() ����·�ʱ���ɶԳ��Կ�֪P(0��-1)��
����·�ʱ���ɶԳ��Կ�֪P(0��-1)��
���ϣ���P������Ϊ(0��1)��(0��-1)��
(2)�����������
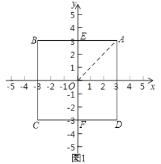
�ٵ�![]() ʱ����ͼ3��M���߶�CD�ϣ���M��MN��AC��N������AM��
ʱ����ͼ3��M���߶�CD�ϣ���M��MN��AC��N������AM��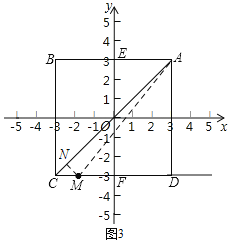
��M���������t��
��CM![]() ��
��
���ı���ABCD�������Σ�
���ACD=45�㣬
���CMN�ǵ���ֱ�������Σ�
��![]() ��
��
��d(M���߶�AC)![]() ��
��
�ڵ�![]() ʱ����ͼ4��M���߶�CD���ӳ����ϣ���M��MN��AC��N��
ʱ����ͼ4��M���߶�CD���ӳ����ϣ���M��MN��AC��N��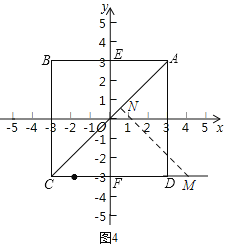
ͬ��![]() ��
��
��d(M���߶�AC)![]() ��
��
���ڶ���M��C��D�������˶�ʱ��MN+MAԽ��Խ��
��![]() ��
��
��ã�![]() ��
��
![]() ��
��
��ã�![]() ��
��
��M�������tȡֵ��Χ��![]() ��
��

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�