题目内容
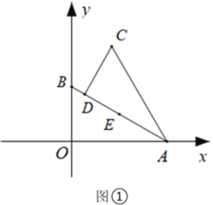
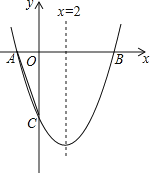
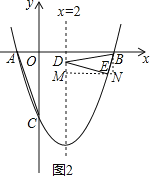
【题目】如图,在平面直角坐标系![]() 中,已知二次函数
中,已知二次函数![]() 图象经过点
图象经过点![]() ,
,![]() ,其对称轴为直线
,其对称轴为直线![]() .
.
(1)求该二次函数的解析式;
(2)若直线![]() 将
将![]() 的面积分成相等的两部分,求
的面积分成相等的两部分,求![]() 的值;
的值;
(3)点![]() 是该二次函数图象与
是该二次函数图象与![]() 轴的另一个交点,点
轴的另一个交点,点![]() 是直线
是直线![]() 上位于
上位于![]() 轴下方的动点,点
轴下方的动点,点![]() 是第四象限内该二次函数图象上的动点,且位于直线
是第四象限内该二次函数图象上的动点,且位于直线![]() 右侧.若以点
右侧.若以点![]() 为直角顶点的
为直角顶点的![]() 与
与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
【答案】(1)抛物线的表达式为:![]() ,直线
,直线![]() 的表达式为:
的表达式为: ![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 坐标为
坐标为![]() 或
或![]() .
.
【解析】
(1)把A、C坐标代入二次函数表达式,再由对称轴公式以及对称轴x=2得到关于a、b、c的方程组,解方程组即可得;
(2)求出直线AC解析式为:![]() ,联立
,联立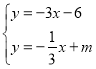 ,求得两直线交点的横坐标为
,求得两直线交点的横坐标为![]() ,直线
,直线 ![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求出
,求出![]() ,
,
由题意得则可知两直线与y轴围成的三角形的面积为 ![]() 且m>-6,解方程即可得;
且m>-6,解方程即可得;
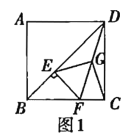
(3)由已知可得![]() ,然后分①当
,然后分①当![]() 时,则
时,则![]() ,如图1,过点
,如图1,过点![]() 作
作![]() 直线
直线![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,根据相似三角形的性质则可得到
,根据相似三角形的性质则可得到![]() ,设点
,设点![]() ,则
,则![]() ,
,![]() ,求得h值即可求得答案;②当
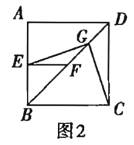
,求得h值即可求得答案;②当![]() 时,
时, ![]() ,过点
,过点![]() 作
作![]() 直线
直线![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则 ![]() ,则可得
,则可得![]() ,设点
,设点![]() ,则
,则![]() ,
, ![]() ,求得p的值即可求得答案.
,求得p的值即可求得答案.
(1)由已知得: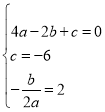 ,解得:
,解得: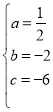 ,
,
故抛物线的表达式为:![]() ;
;
(2)设直线AC解析式为y=k1x+b1,将A(-2,0)、C(0,-6)分别代入得
 ,解得:
,解得: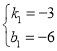 ,
,
所以直线![]() 的表达式为:
的表达式为:![]() ,
,
联立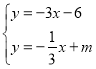 ,解得:
,解得:![]() ,
,
直线 ![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,
∵![]() ,
,
∴由题意得: ![]() ,
,
解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
![]() ;
;
(3)![]() ,
,![]() ,
,
![]() ,
,
①当![]() 时,则
时,则![]() ,
,
如图1,过点![]() 作
作![]() 直线
直线![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
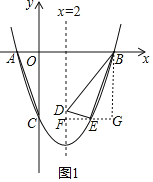
则![]() ,
,
则![]() ,则
,则![]() ,
,
设点![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,即
,即![]() ,
,
![]() 点
点![]() 在二次函数上,故:
在二次函数上,故: ![]() ,
,
解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
则点![]() ;
;
②当![]() 时,
时, ![]() ,
,
过点![]() 作
作![]() 直线
直线![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
则 ![]() ,则
,则![]() ,则
,则![]() ,
,
设点![]() ,则
,则![]() ,
, ![]() ,
,
则![]() ,解得:或
,解得:或![]() (
(![]() 舍去);
舍去);
故点![]() 坐标为
坐标为![]() 或
或![]() .
.

【题目】工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,请将下列过程补充完整:
收集数据:
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:

整理、描述数据:
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70—79分为生产技能良好,60—69分为生产技能合格,60分以下为生产技能不合格)
分析数据:
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | |
乙 | 78 | 81 |
得出结论:
![]() .估计乙部门生产技能优秀的员工人数约为 .
.估计乙部门生产技能优秀的员工人数约为 .
![]() .可以推断出 部门员工的生产技能水平高.理由为 .
.可以推断出 部门员工的生产技能水平高.理由为 .
(至少从两个不同的角度说明推断的合理性)
【题目】某种水果按照果径大小可分为4个等级:标准果、优质果、精品果、礼品果,某采购商从采购的一批该种水果中随机抽取100个,利用它的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
用样本估计总体,果园老板提出两种购销方案给采购商参考,
方案1:不分类卖出,售价为20元/个;
方案2:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/个) | 16 | 18 | 22 | 24 |
(1)从采购商的角度考虑,应该采用哪种购销方案?
(2)若采购商采购的该种水果的进价不超过20元/个,则采购商可以获利,现从这种水果的4个等级中任选2种,按方案2进行购买,求这2种等级的水果至少有一种能使采购商获利的概率.