Question

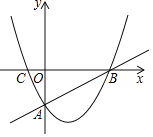
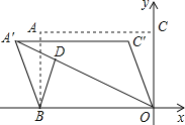
【题目】如图，在平面直角坐标系中，矩形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，AC长为，若将边AC平移至A'C'处，此时A'坐标为（-4，2），分别连接A'B，C'O，反比例函数y=的图象与四边形A'BOC'对角线A'O交于D点，连接BD，则当BD取得最小值时，k的值是______ ．

Answer 1

【答案】-．

【解析】

当BD⊥OA′时，BD取得最小值，延长A′C′交y轴于E，易得△BDO∽△OEA′，结合A'坐标为（-4，2），得==，从而得BD=1，OD=2，作DF⊥OB于F，得DF=，进而得到点D的坐标，即可求解．

当BD⊥OA′时，BD取得最小值，

延长A′C′交y轴于E，如图，

∵A′C′∥OB，

∴A′E⊥y轴，∠BOD=∠EA′O，

∴∠BDO=∠OEA′，

∴△BDO∽△OEA′，

∴==，

∵A'坐标为（-4，2），

∴A′E=4，OE=2，

∴OA′==2，

∵OB=AC=，

∴==，

∴BD=1，OD=2，

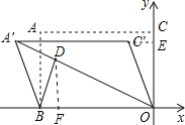
作DF⊥OB于F，

∵BDOD=OBDF，即1×2=DF，

∴DF=，

∴D的纵坐标为，

设直线OA′的解析式为y=kx，

∴2=-4k，解得k=-，

∴直线OA′的解析式为y=-x，

把y=代入得，=-x，解得x=-，

∴D(-，)，

∵反比例函数y=的图象过D点，

∴k=-×=-，

故答案为：-．