题目内容
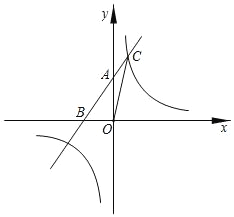
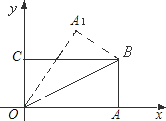
【题目】如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
(A).(4.8,6.4) (B).(4,6) (C)(5.4,5.8) (D).(5,6)
【答案】A
【解析】解:∵BC∥AO,
∴∠BOA=∠OBC,
根据翻折不变性得,
∠A1OB=∠BOA,
∴∠OBC=∠A1OB,
∴DO=DB.
设DO=DB=xcm,
则CD=(8-x)cm,
又∵OC=4,
∴(8-x)2+42=x2,
解得x=5.
∴BD=5,
∴S△BDO=![]() ×5×4=10;
×5×4=10;
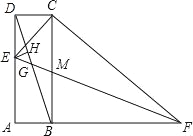
设A1(a,4+b),作A1E⊥x轴于E,交DE于F,如下图所示:
∵BC∥x轴,
∴A1E⊥BC,
∵S△OAB=![]() OAAB=1 2 ×8×4=16,S△BDO=10.
OAAB=1 2 ×8×4=16,S△BDO=10.
∴S△A1BD=![]() BDA1F=1 2 ×5A1F=6,
BDA1F=1 2 ×5A1F=6,
解得A1F=![]() ,
,
∴A点的纵坐标为 ![]() ,
,
∵BD=5,B(8,4)
∴D点坐标为(3,4),
∴过OC两点直线解析式为y=![]() x,
x,
把A点的坐标(a,![]() )代入得,
)代入得,![]() =
=![]() a,
a,
解得a=![]() ,
,

练习册系列答案
相关题目