题目内容
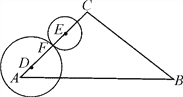
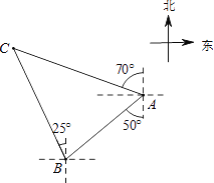
【题目】如图，国家规定休渔期间，我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只，可疑船只正沿北偏西25°方向航行，我国渔政船立即沿北偏西70°方向前去拦截，经过1.5小时刚好在C处拦截住可疑船只，求该可疑船只航行的平均速度．
（结果精确到个位，参考数据： 
≈1.4， 
≈1.7）
【答案】可疑船只航行的平均速度16（海里/小时）．
【解析】
作BD⊥AC于点D，由方向角得出∠ABD=30°、∠CBD=45°，在Rt△ABD中得BD=ABsin∠CAB=10
，在Rt△BCD中求得BC=BD÷cos∠CBD=10
，再除以时间即可得．
如图，作BD⊥AC于点D，
∵∠CBA=25°+50°=75°，∠CAB=（90°﹣70°）+（90°﹣50°）=60°，
∴∠ABD=30°，∠CBD=45°，
在Rt△ABD中，BD=ABsin∠CAB=20×sin60°=20×
=10 ，
在Rt△BCD中，BC=BD÷cos∠CBD=10 ÷cos45°=10÷
=10 ，
∴可疑船只航行的平均速度
≈16（海里/小时）．
练习册系列答案
相关题目
