题目内容
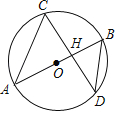
【题目】如图,已知在矩形ABCD中,AB=2,BC=6,点E从点D出发,沿DA方向以每秒1个单位的速度向点A运动,点F从点B出发,沿射线AB以每秒3个单位的速度运动,当点E运动到点A时,E、F两点停止运动.连结BD,过点E作EH⊥BD,垂足为H,连结EF,交BD于点G,交BC于点M,连结CF.
(1)△CDE与△CBF相似吗?为什么?
(2)求证:∠DBC=∠EFC;
(3)同线段GH的值是定值吗?如果不是,请说明理由;如果是,求出这个定值.
【答案】(1)答案见解析 (2)证明见解析 (3)是定值 ![]()
【解析】
(1)根据两边成比例夹角相等两三角形相似即可判断;
(2)想办法证明△DCB∽△ECF,可得∠DBC=∠EFC;
(3)结论:线段GH的值是定值.GH=![]() .由△EDC∽△EHG,可得
.由△EDC∽△EHG,可得![]() =
=![]() ,由AB=DC,可得
,由AB=DC,可得![]() =
=![]() ,想办法用t表示EH,代入化简即可解决问题.
,想办法用t表示EH,代入化简即可解决问题.
(1)∵四边形ABCD是矩形,AD∥BC,AB=DC,
∴∠CDA=∠DCB=∠DAB=∠ABC=90°,
∵![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠CDE=∠FBC=90°
∴△CDE∽△CBF;
(2)证明:∵△CDE∽△CBF,
∴∠DCE=∠BCF,![]() =
=![]() ,
,
∵∠DCE+∠BCE=90°,
∴∠BCE+∠BCF=90°,
∴∠ECF=90°,
∴![]() =
=![]() ,
,
∵∠DCB=∠ECF
∴△DCB∽△ECF,
∴∠DBC=∠EFC.
(3)结论:线段GH的值是定值.GH=![]() .
.
理由:作CN⊥DB于N,
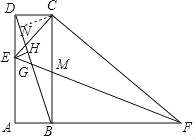
∵AD=BC=6,AB=2,
∴BD=![]() =2
=2![]() ,
,
∵∠EDH=∠ADB,∠EHD=∠DAB,
∴△DEH∽△DBA,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴EH=![]() t,
t,
∵△DCB∽△ECF,
∴∠DBC=∠EFC,
∴∠CDB=∠CEF,
∵∠CDB+∠DCN=90°,∠DCN+∠NCB=90°,
∴∠BDC=∠NCB=∠CEF
∵CN⊥BD,EH⊥DB,
∴CN∥EH,
∴∠NCE=∠CEH,
∴∠ECB=∠HEG,
∵AD∥BC,
∴∠DEC=∠ECB,
∴∠DEC=∠HEG,
∵∠EDC=∠EHG=90°,
∴△EDC∽△EHG,
∴![]() ,
,
∵AB=DC,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴HG=![]() .
.

 阅读快车系列答案
阅读快车系列答案