题目内容
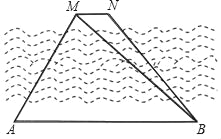
【题目】如图,在一条河的北岸有两个目标M、N,现在位于它的对岸设定两个观测点A、B.已知AB∥MN,在A点测得∠MAB=60°,在B点测得∠MBA=45°,AB=600米.
(1)求点M到AB的距离;(结果保留根号)
(2)在B点又测得∠NBA=53°,求MN的长.(结果精确到1米)
(参考数据:![]() ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
【答案】(1) ![]() ; (2)95m.
; (2)95m.
【解析】
(1)过点M作MD⊥AB于点D,易求AD的长,再由BD=MD可得BD的长,即M到AB的距离;
(2)过点N作NE⊥AB于点E,易证四边形MDEN为平行四边形,所以ME的长可求出,再根据MN=AB-AD-BE计算即可.
解:(1)过点M作MD⊥AB于点D,
∵MD⊥AB,
∴∠MDA=∠MDB=90°,
∵∠MAB=60°,∠MBA=45°,
∴在Rt△ADM中,![]() ;
;
在Rt△BDM中,![]() ,
,
∴BD=MD=![]() ,
,
∵AB=600m,
∴AD+BD=600m,
∴AD+![]() ,
,
∴AD=(300![]() )m,
)m,
∴BD=MD=(900-300![]() )
)![]() ,
,
∴点M到AB的距离(900-300![]() )
)![]() .
.
(2)过点N作NE⊥AB于点E,
∵MD⊥AB,NE⊥AB,
∴MD∥NE,
∵AB∥MN,
∴四边形MDEN为平行四边形,
∴NE=MD=(900-300![]() )
)![]() ,MN=DE,
,MN=DE,
∵∠NBA=53°,
∴在Rt△NEB中,![]() ,
,
∴BE![]() m,
m,
∴MN=AB-AD-BE![]() .
.

练习册系列答案
相关题目