题目内容
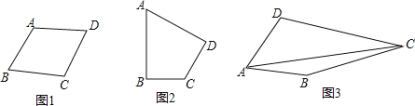
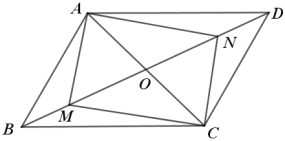
【题目】如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
【答案】(1)见解析;(2)16![]() .
.
【解析】
(1)由平行四边形的性质可知:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形;
(2)根据平行四边形的性质得到AD∥BC,AB=CD=4,求得∠ABC=60°,解直角三角形即可得到结论.
(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,
∴∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∵AB⊥AC,
∴∠BAC=90°,
∴AC=![]() AB=4
AB=4![]() ,
,
∴平行四边形ABCD的面积=ACAB=4![]() 4=16
4=16![]() .
.

练习册系列答案
相关题目