��Ŀ����
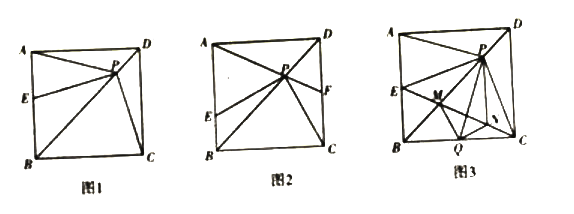
����Ŀ����ͼ1��EΪ����ABCD��AD��һ�㣬��P�ӵ�B������BE��ED��DC�˶�����Cʱֹͣ����Q�ӵ�B��BC�˶�����Cʱֹͣ�������˶����ٶȶ���1cm/s����P��Qͬʱ��ʼ�˶������˶�ʱ��Ϊt��s������BPQ�����Ϊy��cm2������֪y��t�ĺ���ͼ����ͼ2�������н��۴�����ǡ� ��

A��AE=6cm B��![]()
C����0��t��10ʱ��![]() D����t=12sʱ����PBQ�ǵ���������
D����t=12sʱ����PBQ�ǵ���������
���𰸡�D��
����������1������A��ȷ���������£�
��������ͼ���֪��BC=10cm��ED=4cm��
��AE=AD��ED=BC��ED=10��4=6cm��
��2������B��ȷ���������£�
��ͼ������EC������E��EF��BC�ڵ�F��
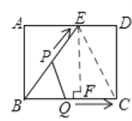
�ɺ���ͼ���֪��BC=BE=10cm��![]() ��
��
��EF=8����![]() ��
��
��3������C��ȷ���������£�
��ͼ������P��PG��BQ�ڵ�G��
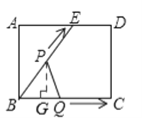
��BQ=BP=t����![]() ��
��
��4������D�������������£�
��t=12sʱ����Q���C�غϣ���P�˶���ED���е㣬
��ΪN����ͼ������NB��NC��

��ʱAN=8��ND=2���ɹ��ɶ�����ã�NB=![]() ��NC=
��NC=![]() ��
��
��BC=10��
���BCN���ǵ��������Σ�����ʱ��PBQ���ǵ�����������
��ѡD��

��ϰ��ϵ�д�
�����Ŀ