题目内容
【题目】(1)下列关于反比例函数y=![]() 的性质,描述正确的有_____。(填所有描述正确的选项)
的性质,描述正确的有_____。(填所有描述正确的选项)
A. y随x的增大而减小
B. 图像关于原点中心对称
C. 图像关于直线y=x成轴对称
D. 把双曲线y=![]() 绕原点逆时针旋转90°可以得到双曲线y=-
绕原点逆时针旋转90°可以得到双曲线y=-![]()
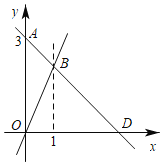
(2)如图,直线AB、CD经过原点且与双曲线y=![]() 分别交于点A、B、C、D,点A、C的横坐标分别为m,n(m>n>0),连接AC、CB、BD、DA。
分别交于点A、B、C、D,点A、C的横坐标分别为m,n(m>n>0),连接AC、CB、BD、DA。
①判断四边形ACBD的形状,并说明理由;
②当m、n满足怎样的数量关系时,四边形ACBD是矩形?请直接写出结论;
③若点A的横坐标m=3,四边形ACBD的面积为S,求S与n之间的函数表达式。

【答案】(1)ABCD;(2)①见解析;②![]() ∴当
∴当![]() 时,四边形ACBD是矩形;
时,四边形ACBD是矩形;
③S=![]()
【解析】
(1)由反比例函数的性质可得.
(2)①根据对称的性质可得四边形ABCD的对角线互相平分,则一定是平行四边形;②由四边形ACBD是矩形时:OA=OC得出 ![]() 利用长度公式得
利用长度公式得![]() 可得关系式:
可得关系式:![]() 整理化简即可。
整理化简即可。
③可得A(3,2)进而求出![]() 的表达式,代入S=
的表达式,代入S=![]() 可得S与n的关系式.
可得S与n的关系式.
解(1)ABCD均正确
(2)①根据对称性可知:OA=OB,OC=OD,则四边形ACBD是平行四边形。
②当四边形ACBD是矩形时:OA=OC
∴![]()
![]()
∵点A、C的横坐标分别为m,n
∴![]()
∴![]()
∴![]()
∴![]()
∵m>n>0
∴![]()
∴当![]() 时,四边形ACBD是矩形
时,四边形ACBD是矩形
③∵![]()
当m=3时,A(3,2)
∴![]()
=![]()
=![]()
=![]()
∴四边形ACBD的面积为S=![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目