题目内容
【题目】如图,过点A(0,3)的一次函数y1=kx+b(k≠0)的图象与正比例函数y2=2x的图象相交于点B,且点B的横坐标是1.
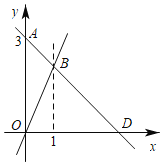
(1)求点B的坐标及k、b的值;
(2)若该一次函数的图象与x轴交于D点,求△BOD的面积
(3)当y1≤y2时,自变量x的取值范围为 .
【答案】(1)B(1,2),![]() ,
,![]() ;(2)△BOD的面积3;(3)x≥1.
;(2)△BOD的面积3;(3)x≥1.
【解析】
(1)先利用正比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式,从而得到k、b的值;
(2)先确定D点坐标,然后利用三角形面积公式计算△BOD的面积;
(3)结合函数图象,写出自变量x的取值范围.
(1)当x=1时,y2=2x=2,则B(1,2),
把A(0,3),B(1,2)代入y=kx+b得
![]() ,解得
,解得![]() ,
,
所以一次函数解析式为y=-x+3;
(2)当x=0时,-x+3=0,解得x=3,则D(3,0),
所以△BOD的面积=![]() ×3×2=3;
×3×2=3;
(3)当y1≤y2时,自变量x的取值范围为x≥1.
故答案为x≥1.

练习册系列答案
相关题目