题目内容
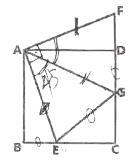
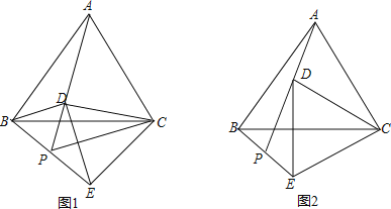
【题目】已知:△ABC是等边三角形,点D是△ABC(包含边界)平面内一点,连接CD,将线段CD绕C逆时针旋转60°得到线段CE,连接BE,DE,AD,并延长AD交BE于点P.
(1)观察填空:当点D在图1所示的位置时,填空:
①与△ACD全等的三角形是______.
②∠APB的度数为______.
(2)猜想证明:在图1中,猜想线段PD,PE,PC之间有什么数量关系?并证明你的猜想.
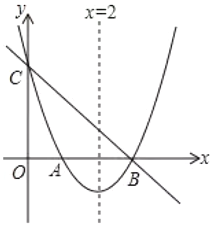
(3)拓展应用:如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.
【答案】(1)①△BCE;②60°;(2)PD+PE=PC,证明见解析;(3)CE的最大值为6.
【解析】
(1)①根据旋转的性质和等边三角形的性质以及全等三角形的判定证明即可;
②根据全等三角形的判定和性质以及三角形内角和解答即可;
(2)根据等边三角形的性质以及全等三角形的判定和性质解答即可;
(3)由(1)可得CE=CD,根据D点在线段AC上,CD长度最小;D点在CA的延长线上,CD的长度最大,求出CD的最大值即可求得线段CE的最大值.
(1)①如图1中,
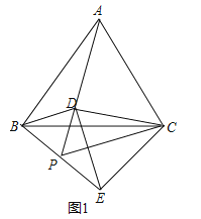
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°,
∵将线段CD绕C顺时针旋转60°得到线段CE,
∴CE=CD,∠DCE=60°,
∴△DCE是等边三角形,
∴∠DCE═60°,
∵∠ACD+∠DCB=60°,∠BCE+∠DCB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS).
故答案为:△BCE.
②∵△ACD≌△BCE,
∴∠EBC=∠DAC,
∵∠DAC+∠BAD=∠BAC=60°,
∴∠PBC+∠BAD=60°,
∴∠APB=180°-∠ABC+∠PBC+∠BAP=180°-60°-60°=60°;
故答案为:60°.
(2)结论:PD+PE=PC.
理由:∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∵∠CAD+∠BAD=60°,∠BAD+∠DBC=60°,
∴∠BAD+∠ABD=∠BDP=60°,
∵∠APB=60°,
∴△BDP是等边三角形,
∴DP=BP,
∴PD+PE=BE,
∵△ADC≌△BEC,
∴AD=BE,
∵在△ABD与△CBP中
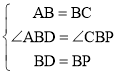 ,
,
∴△ABD≌△CBP(SAS),
∴AD=PC,
∴PD+PE=PC;
(3)如图2中,
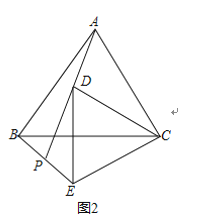
∵AC=4,AD=2,
∴D点在线段AC上,CD长度最小;D点在CA的延长线上,CD的长度最大,
∴4-2≤CD≤4+2,
∴2≤CD≤6.
∴CD的最大值为6,
由(1)可知△ACD≌△BCE,EC=CD,
∴EC的最大值为6.

【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
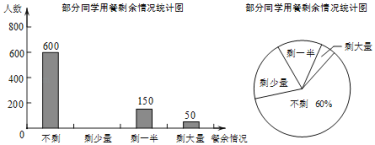
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图

根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.