Question

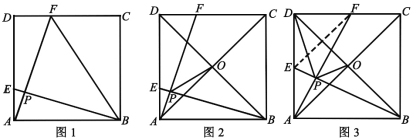
【题目】如图，在正方形中，是边上一点，连接，过作于，交于．

（1）如图1，连接，当，时，求的长；

（2）如图2，对角线，交于点．连接，若，求的长；

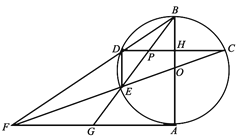
（3）如图3，对角线，交于点．连接，，若，试探索与的数量关系，并说明理由．

Answer 1

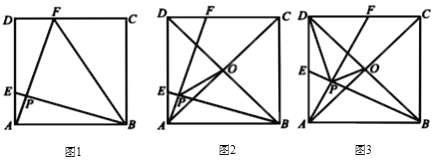
【答案】（1）BF=5；（2）；（3）；理由见解析．

【解析】

（1）根据正方形的性质和已知条件可证明得出△ABE≌△DAF，DF=AE=1，则可得出CF的值，再根据勾股定理即可可得答案.

（2）根据正方形ABCD对角线AC，BD相交于点O，即可得出∠CAB=∠ADB=45°，∠AOB=90°，又于P，∠APB=∠AOB=90°，即A，P，O，B四点共圆，∠OPB=∠OAB=45°，∠OPB=∠ADB ，再根据∠OBP=∠DBE，即可证明得出△OPB∽△EDB，可得，再根据DE=2AE=4，可得AD=AB=6，BD=，，，，即.

（3）连接EF，由（2）可得∠APB=∠AOB=90°，即A，P，O，B四点共圆，∠OPB=∠OAB=45°，∠DPE=∠OPB=45°，再根据A，P，O，B四点共圆有∠POA=∠PBA，则DEP=∠DAB+∠PBA=∠AOB+∠POA=∠POB，再根据∠DPE=∠OPB证明得出△DEP∽△BOP，即，再根据AF⊥BE，∠EDF=90°，得出EDF+∠EPF=180°，D，E，P，F四点共圆，∠DFE=∠DPE=45°，∠DEF=∠DFE=45°，DE=DF ，又AE=DF，于是AE=DE=，，，即可得出.

（1）解：∵正方形ABCD.

∴∠DAB=∠D=∠C=90°，AB=BC=DC=AD=4

∵于P.

∴∠EBA+∠FAB=90°，又∠DAF+FAB=90°．

∴∠EBA=∠DAF

又∠DAB=∠D，AB=DA.

∴△ABE≌△DAF．

∴DF=AE=1，

∴CF=DCDF=3

在Rt△BFC中，.

∴BF=5

（2）∵正方形ABCD对角线AC，BD相交于点O，

∴∠CAB=∠ADB=45°，∠AOB=90°

又于P. ∴∠APB=∠AOB=90°．

∴A，P，O，B四点共圆. ∴∠OPB=∠OAB=45°（也可由相似证得）.

∴∠OPB=∠ADB

又∠OBP=∠DBE，∴△OPB∽△EDB，可得

又DE=2AE=4，可得AD=AB=6，BD=，，，

∴.

∴

（3）

理由如下：连接EF.

∵，由（2）问可知∠APB=∠AOB=90° ，∴A，P，O，B四点共圆，

∴∠OPB=∠OAB=45°，∴∠DPE=∠OPB=45°，

又A，P，O，B四点共圆有∠POA=∠PBA

∴DEP=∠DAB+∠PBA=∠AOB+∠POA=∠POB，

又∠DPE=∠OPB，∴△DEP∽△BOP，

∴

又AF⊥BE，∠EDF=90°，∴EDF+∠EPF=180°，

∴D，E，P，F四点共圆

∴∠DFE=∠DPE=45°，∴∠DEF=∠DFE=45°，有DE=DF

又AE=DF，于是AE=DE=，

∴，

∴