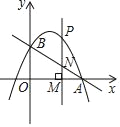题目内容
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的图象与
)的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)用含![]() 的代数式表示点
的代数式表示点![]() 和点
和点![]() 的坐标;
的坐标;
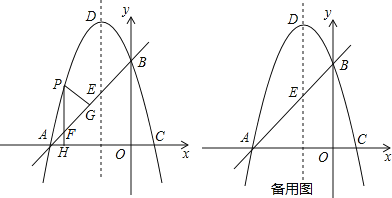
(2)垂直于![]() 轴的直线
轴的直线![]() 在点
在点![]() 与点
与点![]() 之间平行移动,且与抛物线和直线
之间平行移动,且与抛物线和直线![]() 分别交于点
分别交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() .
.
①当![]() 时,求
时,求![]() 的值;
的值;
②若![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
【答案】(1)![]() ,
,![]() ;(2)①3;②当
;(2)①3;②当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.
【解析】
(1)纵坐标为0,横坐标为0,将其直接代入二次函数y=![]() (x-5)(x+m)即可求得坐标.
(x-5)(x+m)即可求得坐标.
(2)①求p的值,通常利用表达式表示p,此时p恰为不含字母的式子.因为t=2,此时p=yN-yM,这里yM为点M的纵坐标,yN为点N的纵坐标;
②求最值也要首先表示p,不过发现因为C为抛物线与直线的交点,在-m≤t≤0,p=yM-yN,当0≤t≤5时,p=yN-yM.如此要分开讨论最值,然后再综合在一起,讨论时不要遗漏题目中关于m的限制:0<m≤1.
解:(1)令![]() ,得
,得![]() ,
,
解得:![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵点![]() 在点
在点![]() 的右侧,
的右侧,
∴![]() ,
,![]() .
.
令![]() ,得
,得![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
(2)①设![]() 的函数关系式为:
的函数关系式为:![]() .
.
把![]() 代入
代入![]() ,解得
,解得![]() ,
,
∴![]() .∵
.∵![]() ,
,
∴点![]() 的纵坐标
的纵坐标![]() ,
,
点![]() 的纵坐标
的纵坐标![]() .
.
∴![]() .
.
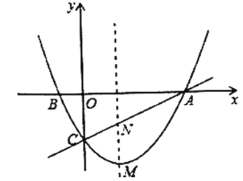
②∵点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,
,
∴点![]() 的纵坐标
的纵坐标![]() ,
,
点![]() 的纵坐标
的纵坐标![]() .
.
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.
当![]() 时
时![]() .
.
此二次函数图象开口向上,对称轴为直线![]() ,
,
∴在![]() 时,
时,![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.
设![]() ,
,![]() 为对称轴,
为对称轴,
∴当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大.
值的增大而增大.
∴![]() 时
时![]() 有最大值3.
有最大值3.
∵![]() ,
,
∴当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某公司有甲种原料![]() ,乙种原料
,乙种原料![]() ,计划用这两种原料生产
,计划用这两种原料生产![]() 、
、![]() 两种产品共40件.生产每件
两种产品共40件.生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润900元;生产每件
,可获利润900元;生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润1100元.设安排生产
,可获利润1100元.设安排生产![]() 种产品
种产品![]() 件(
件(![]() 为非负整数). .
为非负整数). .
(I)根据题意,填写下表:
甲( | 乙( | 件数(件) | |
|
|
| |
|
|
|
(Ⅱ) 安排生产![]() 、
、![]() 两种产品的件数有几种方案?试说明理由:
两种产品的件数有几种方案?试说明理由:
(Ⅲ) 设生产这批40件产品共可获利润![]() 元,将
元,将![]() 表示为
表示为![]() 的函数,并求出最大利润.
的函数,并求出最大利润.