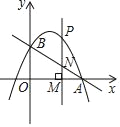题目内容
【题目】已知抛物线![]() .
.
(1)求抛物线![]() 的开口方向、对称轴和顶点坐标;
的开口方向、对称轴和顶点坐标;
(2)将抛物线![]() 向下平移,得抛物线
向下平移,得抛物线![]() ,使抛物线
,使抛物线![]() 的顶点落在直线
的顶点落在直线![]() 上.
上.
①求抛物线![]() 的解析式;
的解析式;
②抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),抛物线
的左侧),抛物线![]() 的对称轴于
的对称轴于![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 是线段
是线段![]() 上的一点,过点
上的一点,过点![]() 作直线
作直线![]() 轴,交抛物线
轴,交抛物线![]() 于点
于点![]() ,点
,点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() ,点
,点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,作
,作![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)抛物线开口向上,对称轴为:直线![]() ,顶点坐标为
,顶点坐标为![]() ;(2)①
;(2)①![]() ;②
;②![]() 点坐标为
点坐标为![]() .
.
【解析】
(1)把二次函数的解析式配成顶点式,即可得到答案;
(2)①设抛物线![]() 的解析式为:
的解析式为:![]() ,把抛物线
,把抛物线![]() 的顶点坐标
的顶点坐标![]() 代入
代入![]() ,求出m的值,即可得到答案;②连接
,求出m的值,即可得到答案;②连接![]() ,由AAS证明
,由AAS证明![]() ,设点
,设点![]() 坐标为
坐标为![]() ,得
,得![]() ,
,![]() ,结合
,结合![]() ,可得关于t的方程,求出t的值,从而求出
,可得关于t的方程,求出t的值,从而求出![]() 的值,进而即可求解.
的值,进而即可求解.
(1)![]() ,
,
∴抛物线开口向上,对称轴为:直线![]() ,顶点坐标为
,顶点坐标为![]() ;
;
(2)①设抛物线![]() 的解析式为:
的解析式为:![]() ,
,
则抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
![]() 抛物线
抛物线![]() 的顶点落在直线
的顶点落在直线![]() 上,
上,
![]() ,解得:
,解得:![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() ;
;
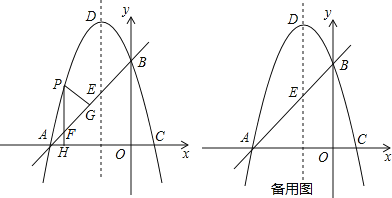
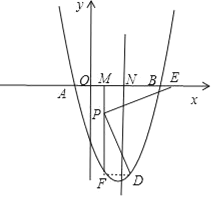
②如图,连接![]() ,
,
由①可得抛物线![]() 的解析式为:
的解析式为:![]() ,
,
令![]() 可得:
可得:![]() ,解得:
,解得:![]() 或
或![]() ,
,
![]() 点
点![]() 在点
在点![]() 的左侧,
的左侧,
![]() ,
,![]() ,
,
![]() 点
点![]() 关于抛物线对称轴对称点为
关于抛物线对称轴对称点为![]() ,且
,且![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
∵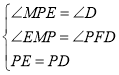
![]() ,
,
![]() ,
,![]() ,
,
设点![]() 坐标为
坐标为![]() ,
,
![]() 点
点![]() 在线段
在线段![]() 上,
上,
![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,解得:
,解得:![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 点坐标为
点坐标为![]() .
.

 计算高手系列答案
计算高手系列答案【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.