题目内容
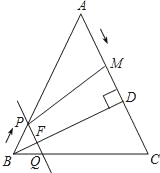
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y(cm2),求y与t之间的函数关系式.
【答案】(1)当t=![]() s时,四边形PQCM是平行四边形;(2)y=
s时,四边形PQCM是平行四边形;(2)y=![]() t2﹣8t+40.
t2﹣8t+40.
【解析】试题分析:(1)假设![]() 为平行四边形,根据平行四边形的性质得到对边平行,进而得到AP=AM,列出关于t的方程,求出方程的解得到满足题意t的值;
为平行四边形,根据平行四边形的性质得到对边平行,进而得到AP=AM,列出关于t的方程,求出方程的解得到满足题意t的值;
(2)根据![]() ,可得△PBQ∽△ABC,根据相似三角形的形状必然相同可知
,可得△PBQ∽△ABC,根据相似三角形的形状必然相同可知![]() 也为等腰三角形,即
也为等腰三角形,即![]() 再由证得的相似三角形得底比底等于高比高,用含
再由证得的相似三角形得底比底等于高比高,用含![]() 的代数式就可以表示出
的代数式就可以表示出![]() ,进而得到梯形的高
,进而得到梯形的高![]() 又点
又点![]() 的运动速度和时间可知点
的运动速度和时间可知点![]() 走过的路程
走过的路程![]() 所以梯形的下底
所以梯形的下底![]() 最后根据梯形的面积公式即可得到
最后根据梯形的面积公式即可得到![]() 与
与![]() 的关系式;
的关系式;
试题解析:(1)假设四边形PQCM是平行四边形,则PM∥QC,
∴AP:AB=AM:AC,
∵AB=AC,
∴AP=AM,即10t=2t,
解得: ![]()
∴当![]() 时,四边形PQCM是平行四边形;
时,四边形PQCM是平行四边形;
(2)∵![]() ,
,
∴△PBQ∽△ABC,
∴△PBQ为等腰三角形,PQ=PB=t,
∴![]() ,即
,即![]()
解得: ![]()
![]()
又∵![]()
![]()

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目