��Ŀ����
����Ŀ��������ȫ�ȵĵȱ������Ρ�ABC�͡�ACDƴ������ABCD����һ����60��ǵ����dz���������ε��ϣ�ʹ���dzߵ�60��ǵĶ������A�غϣ����߷ֱ���AB��AC�غϣ������dz��Ƶ�A����ʱ�뷽����ת��
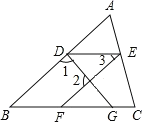
��1�������dzߵ����߷ֱ������ε�����BC��CD�ཻ�ڵ�E��Fʱ������ͼ1����ͨ���۲�����BE��CF�ij��ȣ����ܵó�ʲô���۲�֤����Ľ��ۣ�
��2�������dzߵ����߷ֱ������ε�����BC��CD���ӳ����ཻ�ڵ�E��Fʱ����ͼ2�������ڣ�1���еõ��Ľ��ۻ������𣿼�Ҫ˵�����ɣ�

���𰸡���1��BE��CF������������2��BE��CF��Ȼ���������ɼ�����.
��������
��1������ͼ����BE��CF�ij��ȿ���ֱ�ӵó�BE��CF�Ľ��ۣ���ȻҲ����ͨ��֤����ABE�ա�ACF�ó����ۣ�
��2������ͨ��֤����ADF�ա�ACE���ó�CE��DF�������ó�BE��CF��
��1��BE��CF��
֤�����ڡ�ABE�͡�ACF�У�
�ߡ�BAE+��EAC����CAF+��EAC��60����
���BAE����CAF��
��AB��AC����B����ACF��60�������ABE�ա�ACF��ASA����
��BE��CF��
��2��BE��CF��Ȼ������
֤�����ڡ�ACE�͡�ADF�У�
�ߡ�CAE+��EAD����FAD+��DAE��60����
���CAE����DAF��
�ߡ�BCA����ACD��60����
���FCE��60����
���ACE��120����
�ߡ�ADC��60����
���ADF��120����
�ڡ�ACE�͡�ADF�У�

���ADF�ա�ACE��
��CE��DF��
��BE��CF.