题目内容
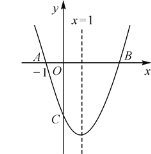
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于A,B两点,与y轴交于点C,且关于直线
轴交于A,B两点,与y轴交于点C,且关于直线![]() 对称,点A的坐标为(-1,0).
对称,点A的坐标为(-1,0).
(1)求二次函数的表达式;
(2)连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度.
【答案】(1)y=x2-2x-3;(2)3-![]() 或3
或3![]() -3.
-3.
【解析】
(1)先根据题意得出点B的坐标,再利用待定系数法求解可得;
(2)分点P在点C上方和下方两种情况,先求出∠OBP的度数,再利用三角函数求出OP的长,从而得出答案.
(1)∵二次函数的对称轴是直线![]() ,
,
∴![]() ,
,
∴b=-2.
将A(-1,0)代入![]() 中,解得
中,解得![]() .
.
∴二次函数的表达式为![]() ;
;
(2)∵A(-1,0),对称轴是直线x=1,
∴点B的坐标为(3,0).
又∵当![]() 时,
时,![]() ,
,
∴点C的坐标为(0,-3),
∴OB=OC,
∴∠OBC=45°.
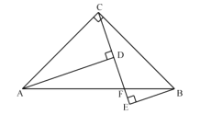
如图,
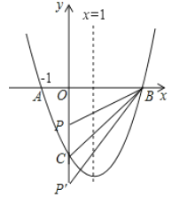
若点P在点C上方,则∠OBP=∠OBC-∠PBC=30°,
∴OP=OBtan∠OBP![]() ,
,
∴CP![]() ;
;
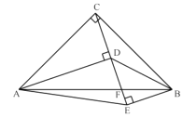
若点P在点C下方,则∠OBP′=∠OBC+∠P′BC=60°,
∴OP′=OBtan∠OBP′![]() ,
,
∴CP′![]() ,
,
综上,线段CP的长度为![]() 或
或![]() .
.

练习册系列答案
相关题目