题目内容
【题目】如图,在平面直角坐标系![]() 中,过
中,过![]() 外一点
外一点![]() 引它的两条切线,切点分别为
引它的两条切线,切点分别为![]() ,
,![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的环绕点.
的环绕点.
(1)当![]() 半径为1时,
半径为1时,
①在![]() ,
,![]() ,
,![]() 中,
中,![]() 的环绕点是_______________;
的环绕点是_______________;
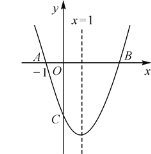
②直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 轴交于点
轴交于点![]() ,若线段
,若线段![]() 上存在
上存在![]() 的环绕点,求
的环绕点,求![]() 的取值范围;
的取值范围;
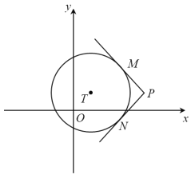
(2)![]() 的半径为1,圆心为
的半径为1,圆心为![]() ,以
,以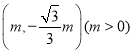 为圆心,
为圆心,![]() 为半径的所有圆构成图形
为半径的所有圆构成图形![]() ,若在图形
,若在图形![]() 上存在
上存在![]() 的环绕点,直接写出
的环绕点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①P1,P3;②![]() 或
或![]() ;(2)-2<t≤4
;(2)-2<t≤4
【解析】
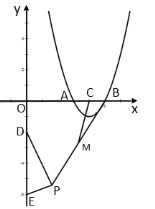
(1)①如图,PM,PN是⊙T的两条切线,M,N为切点,连接TM,TN.当∠MPN=60°时,可证TP=2TM,以T为圆心,TP为半径作⊙T,首先说明:当60°≤∠MPN<180°时,⊙T的环绕点在图中的圆环内部(包括大圆设的点不包括小圆上的点).利用这个结论解决问题即可.
②如图2中,设小圆交y轴的正半轴与于E.求出两种特殊位置b的值,结合图形根据对称性解决问题即可.
(2)如图3中,不妨设E(m,![]() m),则点E在直线y=
m),则点E在直线y=![]() x上,以E(m,
x上,以E(m,![]() m)(m>0)为圆心,
m)(m>0)为圆心,![]() m为半径的⊙E与x轴相切,作⊙E的切线ON,观察图象可知,以E(m,
m为半径的⊙E与x轴相切,作⊙E的切线ON,观察图象可知,以E(m,![]() m)(m>0)为圆心,
m)(m>0)为圆心,![]() m为半径的所有圆构成图形H,图形H即为∠MON的内部,包括射线OM,ON上.利用(1)中结论,画出圆环,当圆环与∠MON的内部有交点时,满足条件,求出两种特殊位置t的值即可解决问题.
m为半径的所有圆构成图形H,图形H即为∠MON的内部,包括射线OM,ON上.利用(1)中结论,画出圆环,当圆环与∠MON的内部有交点时,满足条件,求出两种特殊位置t的值即可解决问题.
(1)①如图,PM,PN是⊙T的两条切线,M,N为切点,连接TM,TN.
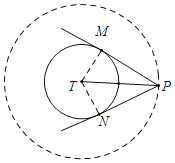
当∠MPN=60°时,∵PT平分∠MPN,
∵∠TPM=∠TPN=30°,
∵TM⊥PM,TN⊥PN,
∴∠PMT=∠PNT=90°,
∴TP=2TM,
以T为圆心,TP为半径作⊙T,
观察图象可知:当60°≤∠MPN<180°时,⊙T的环绕点在图中的圆环内部(包括大圆上的点不包括小圆上的点).
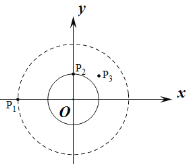
如图中,以O为圆心2为半径作⊙O,观察图象可知,P1,P3是⊙O的环绕点,
故答案为P1,P3.
②如图,设小圆交y轴的正半轴与于E.
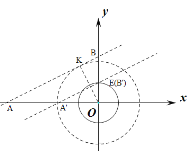
当直线![]() 经过点E时,b=1.
经过点E时,b=1.
当直线![]() 与大圆相切于K(在第二象限)时,连接OK,
与大圆相切于K(在第二象限)时,连接OK,
由题意B(0,b),A(-2b,0),
∴OB=b,OA=2b,![]() ,
,
∵OK=2,![]() ABOK=
ABOK=![]() OAOB,
OAOB,
∴![]() ,
,
解得![]() ,
,
观察图象可知,当![]() 时,线段AB上存在⊙O的环绕点,
时,线段AB上存在⊙O的环绕点,
根据对称性可知:当![]() 时,线段AB上存在⊙O的环绕点,
时,线段AB上存在⊙O的环绕点,
综上所述,满足条件的b的值为![]() 或
或![]() ;
;
(2)如图3中,不妨设E(m,![]() m),则点E在直线y=
m),则点E在直线y=![]() x上,
x上,
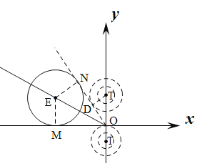
∵m>0,
∴点E在射线OE上运动,作EM⊥x轴,
∵E(m,![]() m),
m),
∴OM=m,EM=![]() ,
,
∴以E(m,![]() m)(m>0)为圆心,
m)(m>0)为圆心,![]() m为半径的⊙E与x轴相切,作⊙E的切线ON,观察图象可知,以E(m,
m为半径的⊙E与x轴相切,作⊙E的切线ON,观察图象可知,以E(m,![]() m)(m>0)为圆心,
m)(m>0)为圆心,![]() m为半径的所有圆构成图形H,图形H即为∠MON的内部,包括射线OM,ON上.
m为半径的所有圆构成图形H,图形H即为∠MON的内部,包括射线OM,ON上.
当⊙T的圆心在y轴的正半轴上时,假设以T为圆心,2为半径的圆与射线ON相切于D,连接TD.
∵![]() ,
,
∴∠EOM=30°,
∵ON,OM是⊙E的切线,
∴∠EON=∠EOM=30°,
∴∠TOD=30°,
∴OT=2DT=4,
∴T(0,4),
当⊙T的圆心在y轴的负半轴上时,且经过点O(0,0)时,T(0,-2),
观察图象可知,当-2<t≤4时,在图形H上存在⊙T的环绕点.