Question

【题目】已知E，F分别是AB、CD上的动点，P也为一动点．

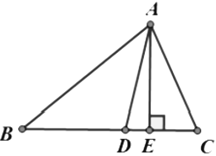
（1）如图1，若AB∥CD，求证：∠P＝∠BEP＋∠PFD；

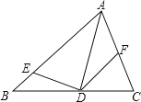
（2）如图2，若∠P＝∠PFD－∠BEP，求证：AB∥CD；

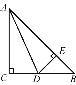
（3）如图3，AB∥CD，移动E，F使得∠EPF＝90°，作∠PEG＝∠BEP，求的值．

Answer 1

【答案】（1）见解析；（2）见解析；（3）2

【解析】

（1）过P作PQ平行于AB，由AB与CD平行，得到PQ与CD平行，利用两直线平行内错角相等得到两对角相等，再由∠EPF=∠1+∠2，等量代换就可得证；

（2）先根据三角形外角的性质得出∠P=∠BGP-∠BEP，再由∠P=∠PGB-∠BEP可知，∠PFD=∠PGB，由此可得出结论；

（3）由（1）中的结论∠EPF=∠BEP+∠PFD，设设∠PFD=x，则∠BEP=90°-x，根据∠PEG=∠BEP=90°-x，利用平角定义表示出∠AEG，即可求出所求比值．

解：（1）过P作PQ∥AB，

∵AB∥CD，

∴PQ∥CD，

∴∠BEP=∠1，∠2=∠PFD，

∵∠EPF=∠1+∠2，

∴∠EPF=∠BEP+∠PFD；

（2）∵∠BGP是△PEG的外角，

∴∠P=∠BGP-∠BEP．

∵∠P=∠PGB-∠BEP，

∴∠PFD=∠PGB，

∴AB∥CD；

（3）由（1）的结论∠EPF=∠BEP+∠PFD=90°，

设∠PFD=x，则∠BEP=90°-x，

∵∠PEG=∠BEP=90°-x，

∴∠AEG=180°-2（90°-x）=2x，则.