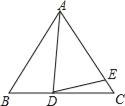
题目内容
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E.
(1)若CD=6![]() ,求AC的长;
,求AC的长;
(2)求证:AB-AC=CD.
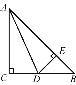
【答案】(1)AC=BC=12+6![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由∠C=90°,AD是∠BAC的角平分线,DE⊥AB,根据角平分线的性质,即可得CD=DE,又由在△ABC中,AC=BC,∠C=90°,根据等腰三角形的性质,可求得AC=BC,∠B=45°,然后利用勾股定理,即可求得AC的长;
(2)首先证得AC=AE,又由(1)易得CD=DE=BE,然后利用线段的和差关系与等量代换的知识,即可求得AB-AC=CD.
(1)∵∠C=90°,AD是∠BAC的角平分线,DE⊥AB,
∴DE=CD=6![]() ,
,
∵在△ABC中,AC=BC,∠C=90°,
∴∠CAB=∠B=45°,
∴∠EDB=∠B=45°,
在Rt△BDE中,由勾股定理得:BD=12
∴AC=BC=CD+BD=12+6![]() ;
;
(2)∵AD是∠BAC的角平分线,
∴∠CAD=∠EAD,
∵∠C=90°,
∴AC⊥BC,
∵DE⊥AB,
∴∠ADC=∠ADE,
又∵AD=AD,
∴△ADC≌△ADE,
∴AE=AC,
∵CD=DE,DE=BE,
∴CD=BE,
∴AB-AC=AB-AE=BE=CD,
即:AB-AC=CD.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目