题目内容
【题目】如图，在
中，
是角平分线，
，
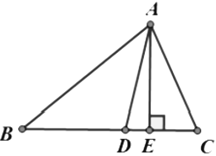
（1）求
的度数．
（2）过点
作
边上的高
， 垂足为
；求
的度数．
【答案】（1）∠BAD=35°；（2）∠EAD=15°．
【解析】
（1）根据三角形内角和定理求出∠BAC的度数，根据角平分线得定义即可求出∠BAD的度数；
（2）由直角三角形两锐角互余的关系可求出∠CAE的度数，根据角平分线的定义可求出∠CAD的度数，根据角的和差关系即可求出∠EAD的度数．
（1）∵∠B=40°，∠C=70°，∠BAC+∠B+∠C=180°，
∴∠BAC=180°-∠B-∠C=70°，
∵
是角平分线，
∴∠BAD=∠CAD=
∠BAC=35°．
（2）∵AE为BC边上的高，
∴∠AEC=90°，
∵∠C=70°，
∴∠CAE=90°-∠C=20°，
∵∠CAD=35°，
∴∠EAD=∠CAD-∠CAE=15°．
练习册系列答案
相关题目
【题目】近年来，共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一，自2016年国庆后，许多高校均投放了使用手机支付就可随取随用的共享单车．某高校为了解本校学生出行使用共享单车的情况，随机调查了某天部分出行学生使用共享单车的情况，并整理成如下统计表．
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
（1）这天部分出行学生使用共享单车次数的中位数是 ，众数是 ，该中位数的意义是 ；
（2）这天部分出行学生平均每人使用共享单车约多少次？（结果保留整数）
（3）若该校某天有1500名学生出行，请你估计这天使用共享单车次数在3次以上（含3次）的学生有多少人？
