题目内容
【题目】如图,在平面直角坐标系xOy中,直线y=﹣ ![]() x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.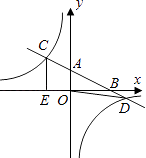
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
(3)x取何值时,反比例函数的值大于一次函数的值.
【答案】
(1)解:∵OE=2,CE⊥x轴于点E.
∴C的横坐标为﹣2,
把x=﹣2代入y=﹣ ![]() x+2得,y=﹣
x+2得,y=﹣ ![]() ×(﹣2)+2=3,
×(﹣2)+2=3,
∴点C的坐标为C(﹣2,3).
设反比例函数的解析式为y= ![]() ,(m≠0)
,(m≠0)
将点C的坐标代入,得3= ![]() .
.
∴m=﹣6.
∴该反比例函数的解析式为y=﹣ ![]() .
.
(2)解:由直线线y=﹣ ![]() x+2可知B(4,0),
x+2可知B(4,0),
解 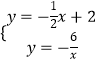 得
得 ![]() ,
, ![]() ,
,
∴D(6,﹣1),
∴S△OBD= ![]() ×4×1=2.
×4×1=2.
(3)由图像可知-2<x<0或x>6
【解析】(1)要求反比例函数的解析式,根据题中的已知条件,CE⊥x轴于点E,OE=2.可知道点C的横坐标为-2,将x=-2代入y=﹣ ![]() x+2可得到点C的纵坐标,用待定系数法可以求出反比例函数的解析式;(2)要求△OBD的面积,就需求出点B和点D的坐标,两函数图像交于点D,建立二元一次方程组,可以求出点D的坐标,直线y=﹣
x+2可得到点C的纵坐标,用待定系数法可以求出反比例函数的解析式;(2)要求△OBD的面积,就需求出点B和点D的坐标,两函数图像交于点D,建立二元一次方程组,可以求出点D的坐标,直线y=﹣ ![]() x+2交x轴于点B,y=0代入即可求得点B的坐标,进而根据三角形的面积公式求得即可。(3)已求出了点D的坐标(6,﹣1),点C的坐标为C(﹣2,3),观察图像可知直线x=-2,y轴,直线x=6将两函数图像分成四个部分,即x<-2,-2<x<0,0<x<6,x>6,观察图像即可得出结论。
x+2交x轴于点B,y=0代入即可求得点B的坐标,进而根据三角形的面积公式求得即可。(3)已求出了点D的坐标(6,﹣1),点C的坐标为C(﹣2,3),观察图像可知直线x=-2,y轴,直线x=6将两函数图像分成四个部分,即x<-2,-2<x<0,0<x<6,x>6,观察图像即可得出结论。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目