题目内容
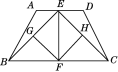
【题目】如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别为BE,BC,CE的中点.
(1)试说明四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF=![]() BC,试说明平行四边形EGFH是正方形.
BC,试说明平行四边形EGFH是正方形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
通过中位线定理得出GF∥EH且GF=EH,所以四边形EGFH是平行四边形;
当添加了条件EF⊥BC,且EF=![]() BC后,通过对角线相等且互相垂直平分(EF⊥GH,且EF=GH)就可证明是正方形.
BC后,通过对角线相等且互相垂直平分(EF⊥GH,且EF=GH)就可证明是正方形.
解:(1)在△BEC中,
∵G,F分别是BE,BC的中点,
∴GF∥EC(即GF∥EH)且GF=![]() EC.
EC.
∵H为EC的中点,∴EH=![]() EC,
EC,
∴GF=EH.
∴四边形EGFH是平行四边形.
(2)连接GH.∵G,H分别是BE,CE的中点,
∴GH∥BC且GH=![]() BC,
BC,
又∵EF⊥BC且EF=![]() BC,
BC,
∴EF⊥GH且EF=GH.
∴平行四边形EGFH是正方形.

练习册系列答案
相关题目
【题目】小明在某商店购买商品A,B共3次,只有一次购买时,商品同时打折,其余两次均按标价购买,三次购买商品A,B的数量和费用如下表:
购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
第一次购买 | 7 | 6 | 1350 |
第二次购买 | 4 | 8 | 1320 |
第三次购买 | 10 | 9 | 1188 |
(1)小明以折扣价购买商品的是第_____次购物;
(2)求商品A,B的标价;
(3)若商品A,B的折扣相同,问商店是打几折出售的这两种商品.






