题目内容
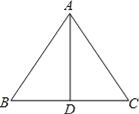
【题目】如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__.
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
【答案】②③④
【解析】解:应添加的条件是②③④;
证明:②当∠BAD=∠CAD时,∵AD是∠BAC的平分线,且AD是BC边上的高,则△ABD≌△ACD,∴△BAC是等腰三角形;
③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF.
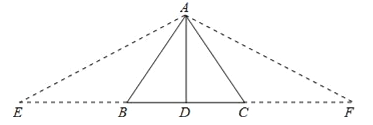
∵AB+BD=CD+AC,∴DE=DF,又AD⊥BC,∴△AEF是等腰三角形,∴∠E=∠F.
∵AB=BE,∴∠ABC=2∠E.
同理,得∠ACB=2∠F,∴∠ABC=∠ACB,即AB=AC,△ABC是等腰三角形;
④△ABC中,AD⊥BC,根据勾股定理,得:
AB2﹣BD2=AC2﹣CD2,即(AB+BD)(AB﹣BD)=(AC+CD)(AC﹣CD).
∵AB﹣BD=AC﹣CD①,∴AB+BD=AC+CD②;
∴①+②得:2AB=2AC,∴AB=AC,∴△ABC是等腰三角形.
故答案为:②③④.

练习册系列答案
相关题目