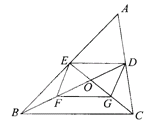
题目内容
【题目】生活中,有人喜欢把传送的便条折成“![]() ”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
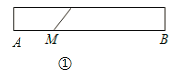

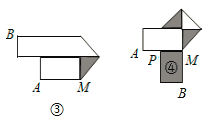
如果由信纸折成的长方形纸条(图①)长为2 6 厘米,分别回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BE=_____厘米; 在图④中,BM=______厘米.
(2)如果长方形纸条的宽为x厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(结果用x表示).
【答案】 21 15
【解析】分析:(1)观察图形,由折叠的性质可得:BE=纸条的长﹣宽﹣AM,BM的长等于②中BE的长﹣2个宽;
(2)根据轴对称的性质,由图可得AP=BM=![]() ,继而可求得在开始折叠时起点M与点A的距离.
,继而可求得在开始折叠时起点M与点A的距离.
详解:(1)图②中BE=26﹣3﹣2=21(厘米),图④中BM=21﹣2×3=15(厘米).
故答案为:21,15;
(2)∵图④为轴对称图形,∴AP=BM=![]() ,∴AM=AP+PM=
,∴AM=AP+PM=![]() +x=13﹣
+x=13﹣![]() x.
x.
即开始折叠时点M与点A的距离是![]() 厘米.
厘米.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目