题目内容
【题目】已知△ABC中,∠C=90°,tanA= ![]() ,D是AC上一点,∠CBD=∠A,则sin∠ABD=( )
,D是AC上一点,∠CBD=∠A,则sin∠ABD=( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:作DE⊥AB于点E. ∵∠CBD=∠A,
∴tanA=tan∠CBD= ![]() =
= ![]() ,
,
设CD=1,则BC=2,AC=4,
∴AD=AC﹣CD=3,
在直角△ABC中,AB= ![]() =
= ![]() =2
=2 ![]() ,
,
在直角△ADE中,设DE=x,则AE=2x,
∵AE2+DE2=AD2 ,
∴x2+(2x)2=9,
解得:x= ![]() ,
,
则DE= ![]() ,AE=
,AE= ![]() .
.
∴BE=AB﹣AE=2 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴tan∠DBA= ![]() =
= ![]() ,
,
∴sin∠DBA= ![]() .
.
故选:A.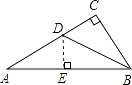
【考点精析】通过灵活运用勾股定理的概念和相似三角形的判定与性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
造型花卉 | 甲 | 乙 |
A | 80 | 40 |
B | 50 | 70 |
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?