题目内容
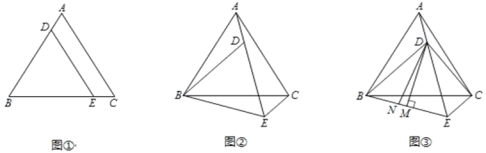
【题目】如图,在等边![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向运动,连接
方向运动,连接![]() ,以
,以![]() 为边,在
为边,在![]() 右侧按如图方式作等边
右侧按如图方式作等边![]() ,当点P从点E运动到点A时,求点F运动的路径长?
,当点P从点E运动到点A时,求点F运动的路径长?

【答案】8
【解析】
连结DE,作FH⊥BC于H,如图,根据等边三角形的性质得∠B=60°,过D点作DE′⊥AB,则BE′=![]() BD=2,则点E′与点E重合,所以∠BDE=30°,DE=
BD=2,则点E′与点E重合,所以∠BDE=30°,DE=![]() ,接着证明△DPE≌△FDH得到FH=DE=2
,接着证明△DPE≌△FDH得到FH=DE=2![]() ,于是可判断点F运动的路径为一条线段,此线段到BC的距离为2
,于是可判断点F运动的路径为一条线段,此线段到BC的距离为2![]() ,当点P在E点时,作等边三角形DEF1,则DF1⊥BC,当点P在A点时,作等边三角形DAF2,作F2Q⊥BC于Q,则△DF2Q≌△ADE,所以DQ=AE=8,所以F1F2=DQ=8,于是得到当点P从点E运动到点A时,点F运动的路径长为8.
,当点P在E点时,作等边三角形DEF1,则DF1⊥BC,当点P在A点时,作等边三角形DAF2,作F2Q⊥BC于Q,则△DF2Q≌△ADE,所以DQ=AE=8,所以F1F2=DQ=8,于是得到当点P从点E运动到点A时,点F运动的路径长为8.
连结DE,作FH⊥BC于H,如图,
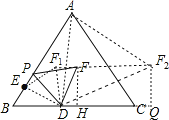
∵△ABC为等边三角形,
∴∠B=60°,
过D点作DE′⊥AB,则BE′=![]() BD=2,
BD=2,
∴点E′与点E重合,
∴∠BDE=30°,DE=![]() BE=2
BE=2![]() ,
,
∵△DPF为等边三角形,
∴∠PDF=60°,DP=DF,
∴∠EDP+∠HDF=90°
∵∠HDF+∠DFH=90°,
∴∠EDP=∠DFH,
在△DPE和△FDH中,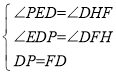 ,
,
∴△DPE≌△FDH,
∴FH=DE=2![]() ,
,
∴点P从点E运动到点A时,点F运动的路径为一条线段,此线段到BC的距离为2![]() ,
,
当点P在E点时,作等边三角形DEF1,∠BDF1=30°+60°=90°,则DF1⊥BC,
当点P在A点时,作等边三角形DAF2,作F2Q⊥BC于Q,则△DF2Q≌△ADE,所以DQ=AE=10-2=8,
∴F1F2=DQ=8,
∴当点P从点E运动到点A时,点F运动的路径长为8.

练习册系列答案
相关题目