题目内容
【题目】如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.

(1)当点E在线段BD上移动时,如图(1)所示,求证:AE=EF;
(2)当点E在直线BD上移动时,如图(2)、图(3)所示,线段AE与EF又有怎样的数量关系?请直接写出你的猜想,不需证明.
【答案】(1)证明见解析;(2)AE=EF,证明见解析.
【解析】
(1)如图1中,在BA上截取BH,使得BH=BE.证明△AHE≌△EDF,根据全等三角形的性质可得AE=EF;(2)如图2中,在BC上截取BH=BE,类比(1)的方法可证AE=EF;如图3中,在BA上截取BH,使得BH=BE.类比(1)的方法可证AE=EF.
(1)证明:如图1中,在BA上截取BH,使得BH=BE.
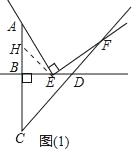
∵BC=AB=BD,BE=BH,
∴AH=ED,
∵∠AEF=∠ABE=90°,
∴∠AEB+∠FED=90°,∠AEB+∠BAE=90°,
∴∠FED=∠HAE,
∵∠BHE=∠CDB=45°,
∴∠AHE=∠EDF=135°,
∴△AHE≌△EDF,
∴AE=EF.
(2)如图2中,在BC上截取BH=BE,同法可证:AE=EF
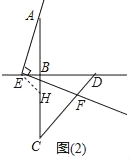
如图3中,在BA上截取BH,使得BH=BE.同法可证:AE=EF.

练习册系列答案
相关题目