题目内容
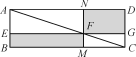
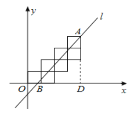
【题目】七个边长为1的正方形按如图所示的方式放置在平面直角坐标系中，直线l经过点A（4，4）和点B，且将这七个正方形的面积分成相等的两部分，则直线l的函数表达式是_______．
【答案】y= 
x-
【解析】
根据题意过点A作AD⊥x轴于点D，由直线l将七个正方形面积分为相等的两部分确定出三角形ABD面积，进而求出BD的长，得出OB的长即为B横坐标，得到B坐标，最后利用待定系数法求出直线l的函数表达式即可．
解：如图，过点A作AD⊥x轴于点D，
由题意，可知△ABD的面积为
，
∴
ADBD=
，即BD= 
= 
，
∴OB=4- = 
，
则点B坐标为
，
设直线l的函数表达式为
，利用待定系数法代入A、B两坐标，
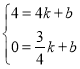，解得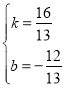
，
故直线l的函数表达式为y= x-.
【题目】重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工，计划10年内解决低收入人群的住房问题，前6年，每年竣工投入使用的公租房面积y（单位：百万平方米），与时间x的关系是y=
x+5，（x单位：年，1≤x≤6且x为整数）；后4年，每年竣工投入使用的公租房面积y（单位：百万平方米），与时间x的关系是y=-
x+
（x单位：年，7≤x≤10且x为整数）．假设每年的公租房全部出租完．另外，随着物价上涨等因素的影响，每年的租金也随之上调，预计，第x年投入使用的公租房的租金z（单位：元/m2）与时间x（单位：年，1≤x≤10且x为整数）满足一次函数关系如下表：
z（元/m2） | 50 | 52 | 54 | 56 | 58 | … |
x（年） | 1 | 2 | 3 | 4 | 5 | … |
（1）求出z与x的函数关系式；
（2）求政府在第几年投入的公租房收取的租金最多，最多为多少百万元；
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年投入的公租房总面积不变的情况下，要让人均住房面积比第6年人均住房面积提高a%，这样可解决住房的人数将比第6年减少1.35a%，求a的值．
（参考数据：
，
，
）
【题目】保险公司车保险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下表：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
该公司随机调查了该险种的300名续保人在一年内的出险情况，得到如下统计图：
(1)样本中，保费高于基本保费的人数为__________名；
(2)已知该险种的基本保费a为6 000元，估计1名续保人本年度的平均保费．
