题目内容
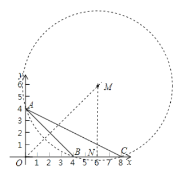
【题目】如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为___________.

【答案】(6,6)
【解析】
如图:由题意可得M在AB、BC的垂直平分线上,则BN=CN;证得ON=OB+BN=6,即△OMN是等腰直角三角形,得出MN=ON=6,即可得出答案.
解:如图∵圆M是△ABC的外接圆
∴点M在AB、BC的垂直平分线上,
∴BN=CN,
∵点A,B,C的坐标分别是(0,4),(4,0),(8,0)
∴OA=OB=4,OC=8,
∴BC=4,
∴BN=2,
∴ON=OB+BN=6,
∵∠AOB=90°,
∴△AOB是等腰直角三角形,
∵OM⊥AB,
∴∠MON=45°,
∴△OMN是等腰直角三角形,
∴MN=ON=6,点M的坐标为(6,6).
故答案为(6,6).

练习册系列答案
相关题目