题目内容
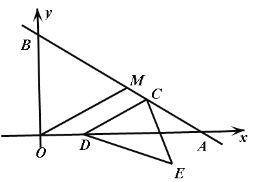
【题目】如图，在平面直角坐标系中，直线分
别交
轴、
轴于点
，交直线
于点
．动点
在直线
上以每秒
个单位的速度从点
向终点
运动，同时，动点
以每秒
个单位的速度从点
沿
的方向运动，当点到达终点时，点同时停止运动．设运动时间为
秒．
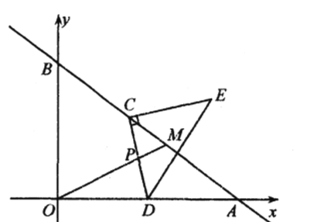
（1）求点的坐标和
的长．
（2）当
时，线段
交
于点
且
求的值．
（3）在点的整个运动过程中，
①直接用含的代数式表示点的坐标．
②利用（2）的结论，以为直角顶点作等腰直角
（点
按逆时针顺序排列）．当与的一边平行时，求所有满足条件的的值．
【答案】（1）
（20，0），
；（2）2；（3）①
（
，
）（
），②
，
或
【解析】
（1）联立两直线解析式，所求得的解即为交点横纵坐标，再根据两点间距离公式求点之间的距离；
（2）过点C作CF⊥OA于F，利用平行线分线段成比例，求出C点坐标，用含有a的表达式表示出D，根据
可知点P为CD中点，利用中点坐标公式表示出点P坐标代入
，即可求得参数a的值；
（3）分三种情况讨论
与
的一边平行情况，用含有t的字母表示各点坐标，根据平行线斜率相等，垂直斜率之积为﹣1建立等量关系，求解t的值．
解：（1）∵直线AB为
，
∴点A（20，0），B（0，15），
∵点M为直线AB：与直线OM：的交点，
∴联立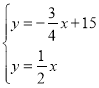
，
解得点M坐标为：（12，6），
∴
，
故答案为：A（20，0），；
（2）过点C作CF⊥OA于F，
由（1）知OA=20，OB=15，
∴
当
时，
，
，
∵BO⊥AO，CF⊥OA，
∴
，
，
∴
，
，
∴
，点C的纵坐标为：
，
∴点C（8，9）， 点D（5a，0），
∵
∴点P为CD的中点，
∴点P（
，
），
∵点P在直线：上，
将点P（，3）代入，
∴得
；
（3）①
，
由（2）图知，，，
∴
，
，
∴
，
∴点C（，）（），
②依题意知，，
∴点D（2t，0），点C（，）
如图，当OM平行CE时，由∠ECD=90°可知CD⊥CE，
根据互相垂直两直线斜率之积为—1，
可得：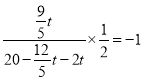
，
解得：
；
如图，当OM∥CD时，两直线斜率相等，
则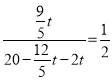
，
解得：
；
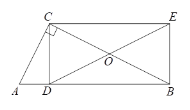
如图，DE∥OM，过点C作CP⊥x轴于P，作CQ平行x轴，过点E作EG⊥x轴于G交CQ于Q，
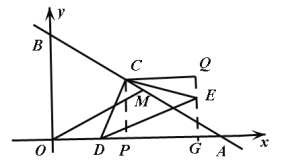
∵△DCE为等腰直角三角形，
∴易证△DPC≌△EQC，
∴
，
，
∴点E的坐标为：（
，
），
由两平行直线，斜率相等得，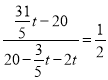
，
解得：
，
综上所述，满足的条件的t的值为：，或．
