题目内容
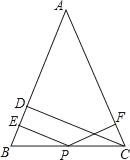
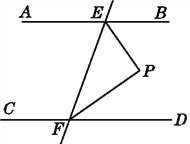
【题目】如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EP平分∠BEF,FP平分∠DFE.试说明:△PEF是直角三角形.
【答案】△PEF是直角三角形
【解析】试题分析：根据平行线的性质，由AB∥CD得到∠BEF＋∠DFE ＝180°，再根据角平分线定义得∠PEF＋∠PFE＝
(∠BEF＋∠DFE)，然后计算出∠P＝90°，根据直角三角形的定义即可得到△EPF是直角三角形．
试题解析：
证明：因为AB∥CD，
所以∠BEF＋∠DFE＝180°．
又因为EP平分∠BEF，FP平分∠DFE，
所以∠PEF＝
∠BEF，∠PFE＝
∠DFE．
所以∠PEF＋∠PFE＝
(∠BEF＋∠DFE)＝90°．
又因为∠PEF＋∠PFE＋∠P＝180°，
所以∠P＝90°．
所以△PEF是直角三角形．
练习册系列答案
相关题目
【题目】某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：
候选人 | 甲 | 乙 | 丙 | 丁 | |
测试成绩 （百分制） | 面试 | 86 | 92 | 90 | 83 |
笔试 | 90 | 83 | 83 | 92 | |
如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们
和
的权．根据四人各自的平均成绩，公司将录取（ ）
A. 甲 B. 乙 C. 丙 D. 丁
