ЬтФПФкШн
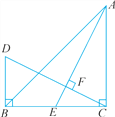
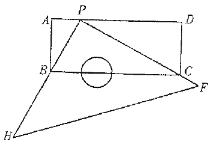
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌACЃН5cmЃЌBCЃН12cmЃЎЖЏЕуPДгAЕуГіЗЂбиAЁњCЕФТЗОЖЯђжеЕуCдЫЖЏЃЛЖЏЕуQДгBЕуГіЗЂбиBЁњCЁњAТЗОЖЯђжеЕуAдЫЖЏЃЎЕуPКЭЕуQЗжБ№вдУПУы1cmКЭ3cmЕФдЫЖЏЫйЖШЭЌЪБПЊЪМдЫЖЏЃЌЦфжавЛЕуЕНДяжеЕуЪБСэвЛЕувВЭЃжЙдЫЖЏЃЌдкФГЪБПЬЃЌЗжБ№Й§ЕуPКЭQзїPEЁЭMNгкEЃЌQFЁЭMNгкFЃЎдђЕуPдЫЖЏЪБМфЮЊ_____УыЪБЃЌЁїPECгыЁїQFCШЋЕШЃЎ
ЁОД№АИЁП![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ИљОнЬтвтЛЏГЩЖўжжЧщПі,ИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіCP=CQ,ДњШыЕУГіЙигкtЕФЗНГЬ,ЧѓГіМДПЩ.
Нт:гЩЬтвтЕУЗжЮЊЖўжжЧщПі:
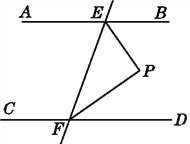
ШчЭМ1, 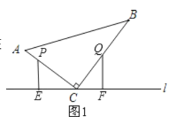
PдкACЩЯ,QдкBCЩЯ,
![]() PEЁЭl,QFЁЭl,
PEЁЭl,QFЁЭl,![]() ЁЯPEC=ЁЯQFC=90
ЁЯPEC=ЁЯQFC=90![]() ,
,
![]() ACB=90
ACB=90![]() ,
,
![]() ЁЯEPC+ЁЯPCE=90
ЁЯEPC+ЁЯPCE=90![]() ,ЁЯPCE+ЁЯQCF=90,
,ЁЯPCE+ЁЯQCF=90,
![]() ЁЯEPC=ЁЯQCF,
ЁЯEPC=ЁЯQCF,
дђЁїPCEЁеЁїCQF,
![]() PC=CQ,
PC=CQ,
МД5-t=12-3t,НтЕУt=![]() ;
;
ЕБPЁЂQОљдкACЩЯЕФЪБКђЃЌДЫЪБ4ЃМtЃМ5ЃЌ
ШчЭМЃК
AP=5-tЃЌCQ=3t-12ЃЌ
![]() 5-t=3t-12ЃЌНтЕУt=
5-t=3t-12ЃЌНтЕУt=![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊ:![]() Лђ
Лђ![]() .
.

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП