��Ŀ����
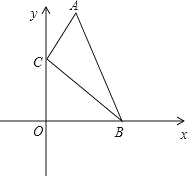
����Ŀ��ij��˾����һ�ֲ�Ʒ����˾��������Ա���±��������ַ�����ͼ��ʾ�����з���һ��ʾͼ���Ƕ���B��ԭ��������ߵ�һ���֣���������ʾͼ�������ߣ�������Ա������Ʒ������Ϊx����������������Ա���±���Ϊy��Ԫ����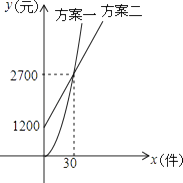
��1���ֱ������ַ�����y����x�ĺ�����ϵʽ��
��2�������۴ﵽ���ټ�ʱ�����ַ����±�����ﵽ3800Ԫ��
��3������˾�����Ľ����������������ֻ������ʲ��䣬ÿ����������mԪ��ʹ�õ�����Ա���۲����ﵽ40��ʱ�����ַ����ı��������1000Ԫ����m��ȡֵ��Χ��
���𰸡�
��1���⣺�� ![]() ���ѣ�30��2700������ã�900a=2700��
���ѣ�30��2700������ã�900a=2700��
��ã�a=3��
�� ![]() ��
��
��y2=kx+b���ѣ�0��1200������30��2700������ã� ![]() ��
��
��ã� ![]() ��
��
��y2=50x+1200��
��2���⣺������ã�30x2����50x+1200��=3800��
��ã� ![]() =50��
=50�� ![]() =
= ![]() ����ȥ����
����ȥ����
�𣺵����۴ﵽ50��ʱ�����ַ����±�����ﵽ3800Ԫ
��3���⣺������Ա���۲����ﵽ40��ʱ��
����һ���±���Ϊ����50+m����40+1200=40m+3200��
���������±���Ϊ��3��402=4800��
������ã�4800����40m+3200����1000����40m+3200��4800��1000��
��ã�15��m��65
����������1������ͼ���ϵĽ������꣨30��2700�����õ����κ�����һ�κ����Ľ���ʽ����2�����ݲ��ﵽ3800Ԫ���õ�һԪ���η��̣��õ������۴ﵽ50��ʱ�����ַ����±�����ﵽ3800Ԫ����3��������Ա���۲����ﵽ40��ʱ���������һ�ͷ������ı��꣬���ݱ��������1000Ԫ�����m��ȡֵ��Χ��