��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�AB��CD��x�ᣬBC��DE��y�ᣬ��AB=CD=4cm��OA=5cm��DE=2cm������P�ӵ�A��������A��B��C·���˶�����Cֹͣ������Q�ӵ�O��������O��E��D��C·���˶�����Cֹͣ����P��Q����ͬʱ�������ҵ�P���˶��ٶ�Ϊ1cm/s����Q���˶��ٶ�Ϊ2cm/s��
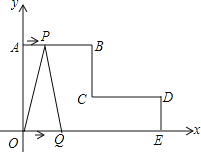
��1��ֱ��д��B��C��D����������ꣻ
��2����P��Q�������![]() sʱ��������PQC�������
sʱ��������PQC�������
��3���������˶���ʱ��Ϊt s����t��ʽ�ӱ�ʾ�˶���������OPQ�����S��
���𰸡���1��B��4��5����C��4��2����D��8��2������2��![]() ����3��S=
����3��S=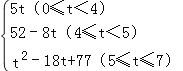 ��
��
��������
�����������1������ƽ��ֱ������ϵд����������꼴�ɣ�
��2���������P��Q�����꣬�����CP��CQ��Ȼ����������ε������ʽ��ʽ���㼴�ɵý⣻
��3���֢�0��t��4ʱ��P��AB�ϣ���Q��OE�ϣ����������������ʽ��ʽ���ɣ�
��4��t��5ʱ����P��BC�ϣ���Q��DE�ϣ�����P��PM��CD��DE���ӳ�����M������S��OPQ=S����OPMB��S��PMQ��S��OEQ����ʽ�������ɣ�
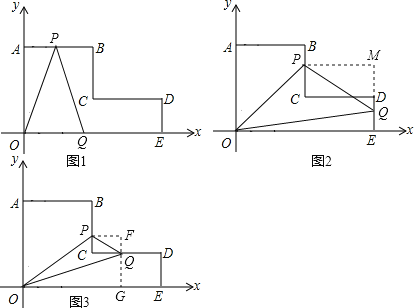
��5��t��7ʱ����P��BC�ϣ���Q��CD�ϣ�����P��PF��CD������Q��QF��OA��PF��F����OE��G��S��OPQ=S����OPFG��S��PFQ��S��OGQ����ʽ�������ɵý⣮
�⣺��1��B��4��5����C��4��2����D��8��2����
��2����t=![]() sʱ����P�˶���·��Ϊ
sʱ����P�˶���·��Ϊ![]() ��
��
��Q�˶���·��Ϊ![]() ��2=11��
��2=11��
���ԣ�P��4��![]() ����Q��7��2����
����Q��7��2����
��CP=![]() ��CQ=3��
��CQ=3��
��S��CPQ=![]() CPCQ=
CPCQ=![]() ��
��![]() ��3=
��3=![]() ��
��
��3��������ã�
�ٵ�0��t��4ʱ������ͼ1��OA=5��OQ=2t��
S��OPQ=![]() OQOA=
OQOA=![]() ��2t��5=5t��
��2t��5=5t��
�ڵ�4��t��5ʱ������ͼ2��OE=8��EM=9��t��PM=4��MQ=17��3t��EQ=2t��8��
S��OPQ=S����OPMB��S��PMQ��S��OEQ��
=![]() ��4+8������9��t����
��4+8������9��t����![]() ��4��17��3t����
��4��17��3t����![]() ��8��2t��8����
��8��2t��8����
=52��8t��
�۵�5��t��7ʱ������ͼ3��PF=14��2t��FQ=7��t��QG=2��OG=18��2t��FG=9��t��
S��OPQ=S����OPFG��S��PFQ��S��OGQ��
=![]() ����14��2t+18��2t������9��t����
����14��2t+18��2t������9��t����![]() ����14��2t����7��t����
����14��2t����7��t����![]() ��18��2t����2��
��18��2t����2��
=t2��18t+77��
����������S=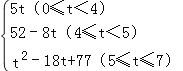 ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�