题目内容
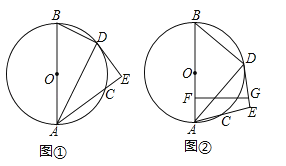
【题目】已知AB是⊙O的直径,C是圆上一点,∠BAC的平分线交⊙O于点D,过D作DE⊥AC交AC的延长线于点E,如图①.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求BD的长;
(3)如图②,若F是OA中点,FG⊥OA交直线DE于点G,若FG=![]() ,tan∠BAD=
,tan∠BAD=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() ;(3)4.
;(3)4.
【解析】试题分析:(1)欲证明DE是⊙O的切线,只要证明OD⊥DE;
(2)首先证明OD⊥BC,在Rt△BDN中,利用勾股定理计算即可;
(3)如图②中,设FG与AD交于点H,根据题意,设AB=5x,AD=4x,则AF=![]() x,想办法用x表示线段FH、GH,根据FH+GH=
x,想办法用x表示线段FH、GH,根据FH+GH=![]() ,列出方程即可解决问题;
,列出方程即可解决问题;
试题解析:解:(1)证明:如图①中,连接OD.∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠OAD=∠DAE,∴∠ODA=∠DAE,∴OD∥AE,∴∠ODE+∠AED=180°,∵∠AED=90°,∴∠ODE=90°,∴OD⊥DE,∴DE是⊙O的切线.
(2)如图①中,连接BC,交OD于点N,∵AB是直径,∴∠BCA=90°,∵OD∥AE,O是AB的中点,∴ON∥AC,且ON=![]() AC,∴∠ONB=90°,且ON=3,则BN=4,ND=2,∴BD=
AC,∴∠ONB=90°,且ON=3,则BN=4,ND=2,∴BD=![]() =
=![]() .
.
(3)如图②中,设FG与AD交于点H,根据题意,设AB=5x,AD=4x,则AF=![]() x,FH=AFtan∠BAD=
x,FH=AFtan∠BAD=![]() x
x![]() =
=![]() x,AH=
x,AH=![]() =
=![]() =
=![]() ,HD=AD﹣AH=4x﹣
,HD=AD﹣AH=4x﹣![]() =
=![]() ,由(1)可知,∠HDG+∠ODA=90°,在Rt△HFA中,∠FAH+∠FHA=90°,∵∠OAD=∠ODA,∠FHA=∠DHG,∴∠DHG=∠HDG,∴GH=GD,过点G作GM⊥HD,交HD于点M,∴MH=MD,∴HM=
,由(1)可知,∠HDG+∠ODA=90°,在Rt△HFA中,∠FAH+∠FHA=90°,∵∠OAD=∠ODA,∠FHA=∠DHG,∴∠DHG=∠HDG,∴GH=GD,过点G作GM⊥HD,交HD于点M,∴MH=MD,∴HM=![]() HD=
HD=![]() ×
×![]() =
=![]() ,∵∠FAH+∠AHF=90°,∠MHG+∠HGM=90°,∴∠FAH=∠HGM,在Rt△HGM中,HG=
,∵∠FAH+∠AHF=90°,∠MHG+∠HGM=90°,∴∠FAH=∠HGM,在Rt△HGM中,HG=![]() =
=![]() =
=![]() ,∵FH+GH=
,∵FH+GH=![]() ,∴
,∴![]() +
+![]() =
=![]() ,解得x=
,解得x=![]() ,∴此圆的半径为
,∴此圆的半径为![]() ×
×![]() =4.
=4.


 阅读快车系列答案
阅读快车系列答案