Question

某市对火车站进行了大规模的改建，改建后的火车站除原有的普通售票窗口外，新增了自动打印车票的无人售票窗口．某日，从早8点开始到上午11点，每个普通售票窗口售出的车票数y₁（张）与售票时间x（小时）的正比例函数关系满足图①中的图象，每个无人售票窗口售出的车票数y₂（张）与售票时间x（小时）的函数关系满足图②中的图象．
（1）图②中图象的前半段（含端点）是以原点为顶点的抛物线的一部分，根据图中所给数据确定抛物线的表达式为　 　，其中自变量x的取值范围是　 　；
（2）若当天共开放5个无人售票窗口，截至上午9点，两种窗口共售出的车票数不少于1450张，则至少需要开放多少个普通售票窗口？
（3）上午10点时，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同，试确定图②中图象的后半段一次函数的表达式．

Answer 1

（1）y=60x²；0≤x≤。
（2）至少需要开放15个普通售票窗口。
（3）y=50x+60。

解析试题分析：（1）设函数的解析式为y=ax²，
把点（1，60）代入解析式得：a=60，则函数解析式为：y=60x²（）。
由图可知，自变量x的取值范围是0≤x≤。
（2）设需要开放x个普通售票窗口，根据售出车票不少于1450，列出不等式解不等式，求最小整数解即可。
（3）求出普通窗口的函数解析式，从而求出10点时售出的票数，和无人售票窗口当x=时，y的值，然后把运用待定系数法求解析式即可。
解：（1）y=60x²；0≤x≤。
（2）设需要开放x个普通售票窗口，
由题意得，80x+60×5≥1450，解得：x≥。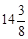
∵x为整数，∴x=15。
∴至少需要开放15个普通售票窗口。
（3）设普通售票的函数解析式为y=kx，
把点（1，80）代入得：k=80，
∴普通售票的函数解析式为y=80x。
∵10点时是x=2，∴当x=2时，y=160。
∴上午10点普通窗口售票为160张。
由（1）得，当x=时，y=135；
又∵上午10点时，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同，
∴图②中的一次函数过点（，135），（2，160）。
设一次函数的解析式为：y=mx+n，
把点的坐标代入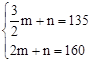得：，解得：。
∴图②中图象的后半段一次函数的表达式为y=50x+60。