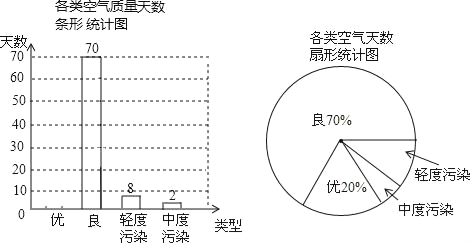
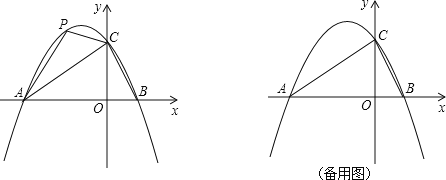题目内容
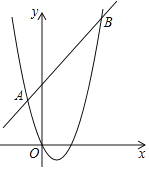
【题目】如图所示,在平面直角坐标系xOy中,有AB为斜边的等腰直角三角形ABC,其中点A(0,2),点C(﹣1,0),抛物线y=ax2+ax﹣2经过B点.
(1)求B点的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否存在点N(点B除外),使得△ACN仍然是以AC为直角边的等腰直角三角形?若存在,求点N的坐标;若不存在,请说明理由.

【答案】(1)(﹣3,1) (2)y=![]() x2+
x2+![]() x﹣2 (3)见解析
x﹣2 (3)见解析
【解析】
(1)根据题意,过点B作BD⊥x轴,垂足为D;根据角的互余的关系,易得B到x、y轴的距离,即B的坐标;
(2)根据抛物线过B点的坐标,可得a的值,进而可得其解析式;
(3)首先假设存在,分A、C是直角顶点两种情况讨论,根据全等三角形的性质,可得答案.
解:(1)过点B作BD⊥x轴,垂足为D.
∵∠BCD+∠ACO=90°,∠ACO+∠CAO=90°,
∴∠BCD=∠CAO,
又∵∠BDC=∠COA=90°,CB=AC,
∴△BCD≌△CAO,
∴BD=OC=1,CD=OA=2,
∴点B的坐标为(﹣3,1);
(2)抛物线y=ax2+ax﹣2经过点B(﹣3,1),
则得到1=9a﹣3a﹣2,
解得a=![]() ,
,
所以抛物线的解析式为y=![]() x2+
x2+![]() x﹣2;
x﹣2;
(3)假设存在点N,使得△ACN仍然是以AC为直角边的等腰直角三角形:
①若以点C为直角顶点;
则延长BC至点N1,使得N1C=BC,得到等腰直角三角形△ACN1,
过点N1作N1M⊥x轴,
∵CN1=BC,∠MCN1=∠BCD,∠N1MC=∠BDC=90°,
∴△MN1C≌△DBC.
∴CM=CD=2,N1M=BD=1,可求得点N1(1,﹣1);
②若以点A为直角顶点;
则过点A作AN2⊥CA,且使得AN2=AC,得到等腰直角三角形△ACN2,
过点N2作N2P⊥y轴,同理可证△AN2P≌△CAO,
∴NP2=OA=2,AP=OC=1,可求得点N2(2,1),
③以A为直角顶点的等腰Rt△ACN的顶点N有两种情况.即过点A作直线L⊥AC,在直线L上截取AN=AC时,点N可能在y轴右侧,即现在解答情况②的点N2;
点N也可能在y轴左侧,即还有第③种情况的点N3.因此,然后过N3作N3G⊥y轴于G,同理:△AGN3≌△CAO,
∴GN3=OA=2,AG=OC=1,
∴N3(﹣2,3);
经检验,点N1(1,﹣1)与点N2(2,1)都在抛物线y=![]() x2+
x2+![]() x﹣2上,点N3
x﹣2上,点N3