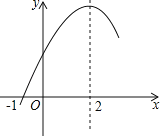Question

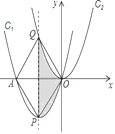
【题目】如图，在平面直角坐标系xOy中，抛物线C1：y1＝（x+3）2﹣，将抛物线C1 向右平移3个单位、再向上平移4.5个单位得抛物线C2，则图中阴影部分的面积为________．

Answer 1

【答案】

【解析】

根据上→加，下→减，左→加，右→减的原则表示抛物线C2的解析式，由对称性可知：S阴影部分=S△OPQ，先计算Q的坐标，表示PQ的长，可得面积．

由平移可得：抛物线C2的解析式：y2=（x+3-3）2-+，
即抛物线C2的解析式：y2=x2，

由抛物线C2的解析式：y2=x2，可知，抛物线C2过原点O，
当x=-3时，y2=×（-3）2=，
∴Q（-3，），
∵抛物线C1：y1＝（x+3）2﹣，

∴P（-3，-），
∴PQ=+=9，P与Q关于x轴对称，
∴OQ=OP，
∴S阴影部分=S△OPQ=×3×PQ=×3×9=．

故答案为：．