题目内容
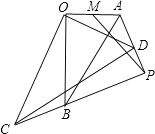
【题目】如图,Rt△AOB∽Rt△DOC,∠ABO=30°,∠AOB=∠COD=90°,M为OA的中点,OA=6,将△COD绕点O旋转一周,直线AD,CB交于点P,连接MP,则MP的最小值是( )
A.6﹣3![]() B.6
B.6![]() -6C.3D.
-6C.3D.![]()
【答案】A
【解析】
根据相似三角形的判定定理证明△COB∽△DOA,得到∠OBC=∠OAD,得到∠APB=∠AOB=90°,求出MS和PS,根据三角形三边关系解答即可.
解:取AB的中点S,连接MS、PS,
则PSMS≤PM≤MS+PS,∵∠AOB=90°,OA=6,∠ABO=30°,
∴AB=2OA=12,OB=![]()
∵∠AOB=∠COD=90°,
∴∠COB=∠DOA,
∵△AOB∽△DOC,
∴![]() ,
,
∴△COB∽△DOA,
∴∠OBC=∠OAD,
∵∠OBC+∠PBO=180°,
∴∠OAD+∠PBO=180°,∠AOB+∠APB=180°,
∴∠APB=∠AOB=90°,又S是AB的中点,
∴PS=![]() AB=6,
AB=6,
∵M为OA的中点,S是AB的中点,
∴MS=![]() OB=3
OB=3![]() ,
,
∴MP的最小值为63![]() ,
,
故选:A.

练习册系列答案
相关题目