Question

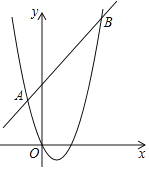
【题目】在平面直角坐标系中，抛物线N过A(﹣1，3)，B(4，8)，O(0，0)三点

(1)求该抛物线和直线AB的解析式.

(2)平移抛物线N，求同时满足以下两个条件的平移后的抛物线解析式：①平移后抛物线的顶点在直线AB上；②设平移后抛物线与y轴交于点C，如果S△ABC＝3S△ABO.

Answer 1

【答案】(1)y＝x2﹣2x；y＝x+4；(2)平移后的抛物线解析式为y＝(x+4)2或y＝(x﹣3)2+7.

【解析】

(1)利用待定系数法求抛物线M和直线AB的解析式；

(2)先求出直线AB与y轴的交点坐标为(0，4)，设平移后抛物线的顶点坐标为(t，t+4)，则平移后的抛物线解析式为y＝(x﹣t)2+t+4，接着表示出N(0，t2+t+4)，利用三角形面积公式得到|t2+t+4﹣4|(4+1)＝4××4×(4+1)，然后解绝对值方程求出得到平移后的抛物线解析式.

解：(1)设抛物线解析式为y＝ax2+bx+c，

把A(﹣1，3)，B(4，8)，O(0，0)代入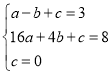得 ，解得，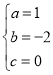

∴抛物线解析式为y＝x2﹣2x；

设直线AB的解析式为y＝mx+n，

把A(﹣1，3)，B(4，8)代入得，解得m＝1，n＝4，

∴直线AB的解析式为y＝x+4；

(2)当x＝0时，y＝x+4＝4，则直线AB与y轴的交点坐标为(0，4)，

设平移后抛物线的顶点坐标为(t，t+4)，则平移后的抛物线解析式为y＝(x﹣t)2+t+4，

当x＝0时，y＝(0﹣t)2+t+4＝t2+t+4，则C(0，t2+t+4)，

∵S△ABC＝3S△ABO，

∴|t2+t+4﹣4|(4+1)＝3××4×(4+1)，

即|t2+t|＝12，

方程t2+t＝﹣12没有实数解，

解方程t2+t＝12得t1＝﹣4，t2＝3，

∴平移后的抛物线解析式为y＝(x+4)2或y＝(x﹣3)2+7.