题目内容
如图在平面直角坐标系内,以点C(1,1)为圆心,2为半径作圆,交x轴于A、B两点,开口向下的抛物线经过A、B两点,且其顶点P在⊙C上。
(1)写出A、B两点的坐标;
(2)确定此抛物线的解析式;
(1) A(1-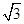 ,0),B(1+
,0),B(1+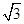 ,0);(2)y=-x2+2x+2.
,0);(2)y=-x2+2x+2.
解析试题分析:(1)过C作AB的垂线,设垂足为H,在Rt△CAH中,已知圆的半径和CH的长(由C点坐标获得),利用勾股定理即可求得AH的长,进而可得到点A的坐标,B点坐标的求法相同.
(2)根据抛物线和圆的对称性知:C、P都在弦AB的垂直平分线上,已知了C点坐标和圆的半径,即可得到点P的坐标,而P为抛物线顶点,可将所求抛物线设为顶点坐标式,然后将A点坐标代入抛物线的解析式中,即可求得待定系数的值,从而求出该抛物线的解析式.
试题解析:(1)过点C作CH⊥x轴,H为垂足;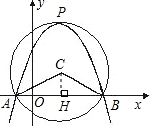
又∵C(1,1),
∴CH=OH=1;(1分)
∴在Rt△CHB中,HB=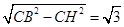 ;
;
∵CH⊥AB,CA=CB,
∴AH=BH;
故A(1-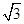 ,0),B(1+
,0),B(1+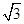 ,0).
,0).
(2)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3);
∴设抛物线解析式为y=a(x-1)2+3,
由已知得抛物线经过点B(1+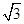 ,0),
,0),
把点B(1+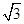 ,0)代入上式,
,0)代入上式,
解得a=-1,
∴抛物线的解析式为:y=-x2+2x+2.
考点: 二次函数综合题

某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表:(不需化简)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | | 40 |
| 销售量(件) | 200 | | |

 与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
 ;
; 的面积为
的面积为 时,求
时,求 的值.
的值. .
.
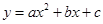 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD= .
. ,
, .设
.设 米,
米, 米.
米.
 与
与 之间的函数解析式;
之间的函数解析式; ?
? ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。
