题目内容
已知抛物线的解析式为
(1)求证:不论m为何值,此抛物线与x轴必有两个交点,且两交点A、B之间的距离为定值;
(2)设点P为此抛物线上一点,若△PAB的面积为8,求符合条件的点P的坐标;
(3)若(2)中△PAB的面积为S(S>0),试根据面积S值的变化情况,确定符合条件的点P的个数(本小题直接写出结论,不要求写出计算、证明过程).
(1)证明见解析;(2)(m,4)或(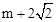 ,?4)或(
,?4)或(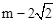 ,-4);(3)当s=8时,符合条件的点P有3个,当0<s<8时,符合条件的点P有4个,当s>8时,符合条件的点P有2个.
,-4);(3)当s=8时,符合条件的点P有3个,当0<s<8时,符合条件的点P有4个,当s>8时,符合条件的点P有2个.
解析试题分析:(1)本题需先求出△的值,再证出△>0,再设出A、B的坐标,然后代入公式即可求出AB的长;
(2)本题需先设出P的坐标,再由题意得出b的值,然后即可求出符合条件的所有点P的坐标;
(3)本题需分当s=8时,当0<s<8时,当s>8时三种情况进行讨论,即可得出符合条件的点P的个数.
试题解析::(1)∵△=(2m)2-4×(-1)(4-m2)=16>0,
∴不论m取何值,此抛物线与x轴必有两个交点.
设A(x1,0),B(x2,0),
则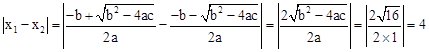 (定值).
(定值).
(2)设P(a,b),则由题意b=-a2+2am+4-m2,且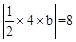 ,
,
解得b=±4.
当b=4时得:a=m,即P(m,4);
当b=-4时得: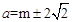 ,即P(
,即P(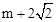 ,?4)或P(
,?4)或P(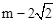 ,-4).
,-4).
综上所述,符合条件的点P的坐标为(m,4)或(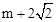 ,?4)或(
,?4)或(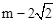 ,-4).
,-4).
(3)由(2)知当s=8时,符合条件的点P有3个,当0<s<8时,符合条件的点P有4个,当s>8时,符合条件的点P有2个.
考点:1.二次函数的和性质;2.曲线上点的坐标与方程的关系;3.分类思想的应用.

练习册系列答案
相关题目


 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.

 的代数式表示);
的代数式表示); 元,此时的销售量是多少?(用含
元,此时的销售量是多少?(用含 与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
 x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
 与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.