��Ŀ����
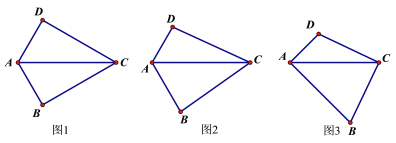
����Ŀ��(1)���֣���ͼ1����AΪ�߶�BC��һ���㣬��BC��a��AB��b����գ�
����Aλ���� ��ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ�� ��(�ú�a��b��ʽ�ӱ�ʾ)
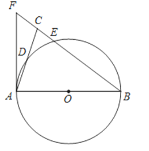
(2)Ӧ�ã���AΪ�߶�BC��һ���㣬��BC��4��AB��1����ͼ2��ʾ���ֱ���AB��ACΪ�ߣ����ȱ�������ABD�͵ȱ�������ACE������CD��BE��
�����ҳ�ͼ����BE��ȵ��߶Σ���˵�����ɣ���ֱ��д���߶�BE�������ֵ��
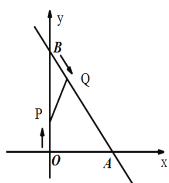
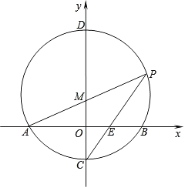
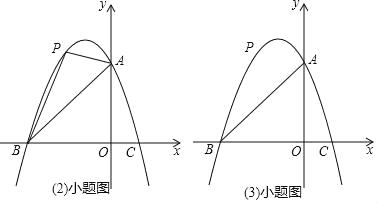
(3)��չ����ͼ3����ƽ��ֱ������ϵ�У���A������Ϊ(2��0)����B������Ϊ(6��0)����PΪ�߶�AB��һ���㣬��PA��2��PM��PB����BPM��90�㣬��ֱ��д���߶�AM�������ֵ����ʱ��P�����꣮
���𰸡�(1)CB���ӳ����ϣ� a+b��(2)��CD��BE�����ɼ���������BE�������ֵΪ5��(3)���������ĵ�P����(2��![]() ��
��![]() )��(2��
)��(2��![]() ����
����![]() )��AM�����ֵΪ2
)��AM�����ֵΪ2![]() +4��
+4��
��������
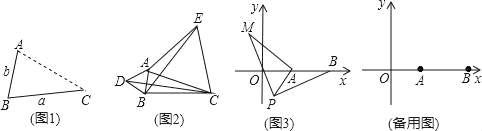
��1�����ݵ�Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�����ɵõ����ۣ���2����������֪������֤��CAD�ա�EAB������ȫ�������ε����ʼ��ɵ�CD��BE���������߶�BE�������ֵ���߶�CD�����ֵ�����ݣ�1���еĽ��ۼ��ɵõ��������3������BM������APM���ŵ�P˳ʱ����ת90��õ���PBN������AN���õ���APN�ǵ���ֱ�������Σ�����ȫ�������ε����ʵõ�PN��PA��2��BN��AM�����ݵ�N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ�����ɵõ����ֵΪ2![]() +4����ͼ2����P��PE��x����E�����ݵ���ֱ�������ε����ʼ�����õ�P�����꣮��ͼ3�У����ݶԳ��Կ�֪����P�ڵ�������ʱҲ�����������ɴ���÷�����������P��һ����������
+4����ͼ2����P��PE��x����E�����ݵ���ֱ�������ε����ʼ�����õ�P�����꣮��ͼ3�У����ݶԳ��Կ�֪����P�ڵ�������ʱҲ�����������ɴ���÷�����������P��һ����������
(1)�ߵ�AΪ�߶�BC��һ���㣬��BC��a��AB��b��
�൱��Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪBC+AB��a+b��
�ʴ�Ϊ��CB���ӳ����ϣ�a+b��
(2)��CD��BE��
���ɣ��ߡ�ABD���ACE�ǵȱ������Σ�
��AD��AB��AC��AE����BAD����CAE��60�㣬
���BAD+��BAC����CAE+��BAC��
����CAD����EAB��
�ڡ�CAD���EAB�У�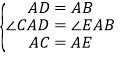 ��
��
���CAD�ա�EAB(SAS)��
��CD��BE��
�����߶�BE�������ֵ���߶�CD�����ֵ��
��(1)֪�����߶�CD�ij�ȡ�����ֵʱ����D��CB���ӳ����ϣ�
�����ֵΪBD+BC��AB+BC��5��
(3)��ͼ1��
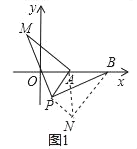
�߽���APM���ŵ�P˳ʱ����ת90��õ���PBN������AN��
���APN�ǵ���ֱ�������Σ�
��PN��PA��2��BN��AM��
��A������Ϊ(2��0)����B������Ϊ(6��0)��
��OA��2��OB��6��
��AB��4��
���߶�AM�������ֵ���߶�BN�������ֵ��
�൱N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ��
���ֵ��AB+AN��
��AN��![]() AP��2
AP��2![]() ��
��
�����ֵΪ2![]() +4��
+4��
��ͼ2��
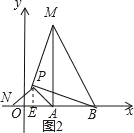
��P��PE��x����E��
�ߡ�APN�ǵ���ֱ�������Σ�
��PE��AE��![]() ��
��
��OE��BO��AB��AE��6��4��![]() ��2��
��2��![]() ��
��
��P(2��![]() ��
��![]() )��
)��
��ͼ3�У�
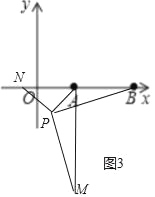
���ݶԳ��Կ�֪����P�ڵ�������ʱ��P(2��![]() ����
����![]() )ʱ��Ҳ����������
)ʱ��Ҳ����������
�������������������ĵ�P����(2��![]() ��
��![]() )��(2��
)��(2��![]() ����
����![]() )��AM�����ֵΪ2
)��AM�����ֵΪ2![]() +4��
+4��

 ��У����ϵ�д�
��У����ϵ�д�