题目内容
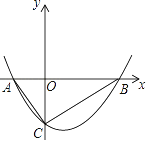
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x轴交于点A,与y轴交于点B.动点P、Q分别从O、B同时出发,其中点P以每秒4个单位的速度沿OB向终点B运动,点Q以每秒5个单位的速度沿BA向终点A运动.设运动时间为t秒.
与x轴交于点A,与y轴交于点B.动点P、Q分别从O、B同时出发,其中点P以每秒4个单位的速度沿OB向终点B运动,点Q以每秒5个单位的速度沿BA向终点A运动.设运动时间为t秒.
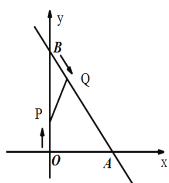
(1)连结PQ,若△AOB和以B、P、Q为顶点的三角形相似,求t的值;
(2)连结AP、OQ,若AP⊥OQ,求t的值;
(3)试证明:PQ的中点在△AOB的一条中位线上.
【答案】(1)当t=1或t=![]() 时,△AOB和以B、P、Q为顶点的三角形相似;(2)t=
时,△AOB和以B、P、Q为顶点的三角形相似;(2)t=![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)根据一次函数解析式求出A、B坐标,得到OA、OB的值,然后分情况讨论:①当![]() 时,△BPQ∽△BOA;②当
时,△BPQ∽△BOA;②当![]() 时,△BPQ∽△BAO,根据比例式,分别代入数据求出t值即可;
时,△BPQ∽△BAO,根据比例式,分别代入数据求出t值即可;
(2)过点Q作QC⊥y轴,垂足为C,根据△BCQ∽△BOA可求出CQ=3t,CO=8-4t,然后根据AP⊥OQ利用同角的余角相等证明∠CQO=∠APO,进而得到△AOP∽△OCQ,根据相似三角形的性质列出比例式求解即可;
(3)首先求出P(0,4t)、Q(3t,8-4t),可得PQ中点的坐标为(![]() ,4),由△AOB的一条中位线所在直线为y=4可得结论.
,4),由△AOB的一条中位线所在直线为y=4可得结论.
解:(1)令y=0,则![]() ,
,
解得:x=6,
∴A(6,0),则OA=6,
令x=0,则y=8,
∴B(0,8),则OB=8,
∵∠AOB=90°
∴AB=![]() ,
,
由已知得OP=4t,BQ=5t,
∴BP=8-4t,
∵∠OBA=∠PBQ,
∴分两种情况讨论
①当![]() 时,△BPQ∽△BOA,
时,△BPQ∽△BOA,
∴![]() ,解得t=1;
,解得t=1;
②当![]() 时,△BPQ∽△BAO,
时,△BPQ∽△BAO,
∴![]() ,解得t=
,解得t=![]() ,
,
综上所述,当t=1或t=![]() 时,△AOB和以B、P、Q为顶点的三角形相似;
时,△AOB和以B、P、Q为顶点的三角形相似;
(2)过点Q作QC⊥y轴,垂足为C,
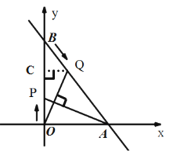
则CQ//OA,
∴△BCQ∽△BOA,
∴![]() ,
,
∴![]() ,
,
解得:BC=4t,CQ=3t,
∵∠QCO=90°,
∴∠CQO+∠COQ=90°,
∵AP⊥OQ,
∴∠COQ+∠APO=90°,
∴∠CQO=∠APO,
∴△AOP∽△OCQ ,
∴![]() ,
,
∴![]()
解得t=![]() ;
;

(3)由(2)得BC=4t,CQ=3t,OC=8-4t,
∴P(0,4t)、Q(3t,8-4t),
∴PQ中点的坐标为(![]() ,4),
,4),
∵△AOB的一条中位线所在直线为y=4,
∴PQ的中点在△AOB的一条中位线上.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案