题目内容
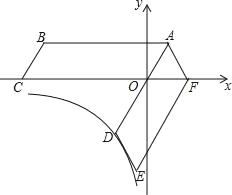
【题目】如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将平行四边形 ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上.若点D在反比例函数y=![]() (x<0)的图象上,则k的值为( )
(x<0)的图象上,则k的值为( )
A.4![]() B.12C.8
B.12C.8![]() D.6
D.6
【答案】A
【解析】
结合图形可知,作DM⊥x轴,MO为横坐标,MD为纵坐标,则求点D坐标转化为求MO和MD的长度;已知四边形ADEF是由四边形ABCO旋转而来,则∠BAO=∠OAF,AO=AF,根据平行四边形性质可知AB∥OC,则可得∠BAO=∠AOF,进而可得∠AOF=60°=∠DOM;根据OA=2,AB=6可得OD=4,再通过三角函数即可求出MO和MD,据此可得答案.
解:如图,作DM⊥x轴,

由题意∠BAO=∠OAF,AO=AF,AB∥OC,
∴∠BAO=∠AOF=∠OAF=∠AFO,
∴∠AOF=60°=∠DOM.
∵OD=AD-OA=AB-OA=6-2=4,
∴∠ODM=30,
∴MO=2,MD=![]() =2
=2![]() ,
,
∴D(-2,-2![]() ),
),
∴k=-2×(-2![]() )=4
)=4![]() .
.
故选A.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】已知二次函数y=﹣x2+bx+c,函数值y与自变量x之间的部分对应值如下表:
x | … | ﹣4 | ﹣1 | 0 | 1 | … |
y | … | ﹣2 | ﹣1 | ﹣2 | ﹣7 | … |
(1)此二次函数图象的对称轴是直线,此函数图象与x轴交点个数为 .
(2)求二次函数的函数表达式;
(3)当﹣5<x<﹣1时,请直接写出函数值y的取值范围.