Question

【题目】如图1，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上，∠AEF=90°，AE=EF，过点F作射线BC的垂线，垂足为H，连接AC．

（1）试判断BE与FH的数量关系，并说明理由；

（2）求证：∠ACF=90°；

（3）如图2，过A、E、F三点作圆，若EC=4，∠CEF=15°，求AE的长．

Answer 1

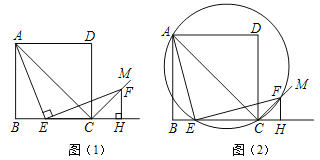
【答案】（1）BE=FH（2）证明见解析（3）2π

【解析】

试题分析：（1）由△ABE≌△EHF（SAS）即可得到BE=FH

（2）由（1）可知AB=EH，而BC=AB，FH=EB，从而可知△FHC是等腰直角三角形，∠FCH为45°，而∠ACB也为45°，从而可证明

（3)由已知可知∠EAC=30°，AF是直径，设圆心为O，连接EO，过点E作EN⊥AC于点N，则可得△ECN为等腰直角三角形，从而可得EN的长，进而可得AE的长，得到半径，得到所对圆心角的度数，从而求得弧长.

试题解析：（1）BE=FH．

理由：∵∠AEF=90°，∠ABC=90°，

∴∠HEF+∠AEB=90°，∠BAE+∠AEB=90°，

∴∠HEF=∠BAE，

在△ABE和△EHF中，

，

∴△ABE≌△EHF（AAS）

∴BE=FH．

（2）由（1）得BE=FH，AB=EH，

∵在正方形ABCD中，BC=AB，∴BE=CH，

∴CH=FH，∴∠HCF=45°，

∵四边形ABCD是正方形，∴∠ACB=45°，

∴∠ACF=180°﹣∠HCF﹣∠ACB=90°．

（3）由（2）知∠HCF=45°，∴CF=FH．

∠CFE=∠HCF﹣∠CEF=45°﹣15°=30°．

如图2，过点C作CP⊥EF于点P，

则CP=CF=FH．

∵∠CEP=∠FEH，∠CPE=∠FHE=90°，

∴△CPE∽△FHE．

∴，即，

∴EF=,

∵△AEF为等腰直角三角形，∴AF=8．

连结AF，取AF中点O，连结接OE，

∵∠AEF=90°，∴AF为⊙O的直径，

则OE=OA=4，∠AOE=90°，

∴AE的长为：．